都立高校入試の令和4年度の過去問から、数学の大問4(平面図形)を解説します。
角の大きさを求める問題
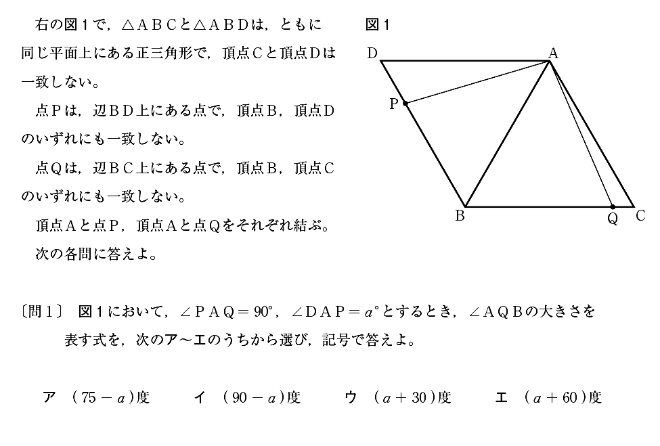
[問1]は∠AQBの大きさを求める問題です。まずは、わかる角度を図に書き込んでいきましょう。
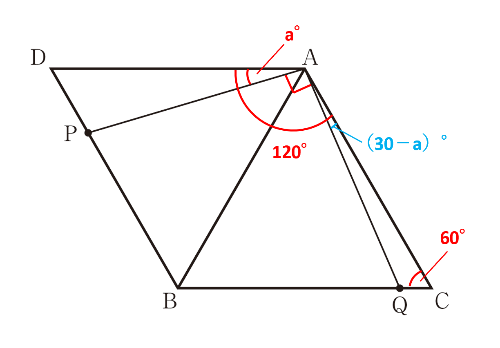
赤で書き込んだ角度は問題文で与えられている情報です。△ABCと△ABDはどちらも正三角形なので、∠ACQ=60°、∠DAC=∠DAB+∠CAB=60+60=120(°)です。
青で書き込んだ角度は∠CAQ=∠DAC-∠DAP-∠PAQ=120-a-90=30-a(°)です。
△ACQの内角と外角の関係から、∠AQB=∠CAQ+∠ACQ=(30-a)+60=90-a(°)となり、イが答えです。
【別解】四角形の内角の和を利用する解き方
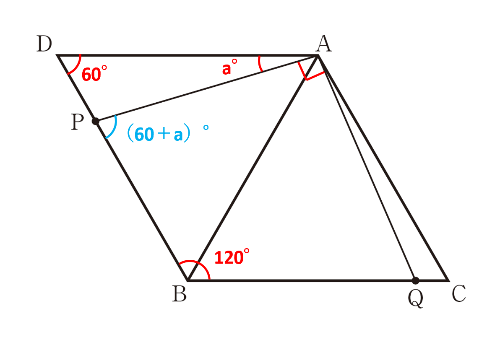
赤で書き込んだ角度は問題文で与えられている情報です。△ABCと△ABDはどちらも正三角形なので、∠ADP=60°、∠PBQ=∠ABP+∠ABQ=60+60=120(°)です。
青で書き込んだ角度は、△ADPの内角と外角の関係から、∠APB=∠ADP+∠DAP=60+a(°)です。
四角形APBQの内角の和は360°なので、∠AQB=360-∠APB-∠PBQ-∠PAQ=360-(60+a)-120-90=90-a(°)となり、イが答えです。
正三角形の性質を利用して三角形の合同を証明する問題
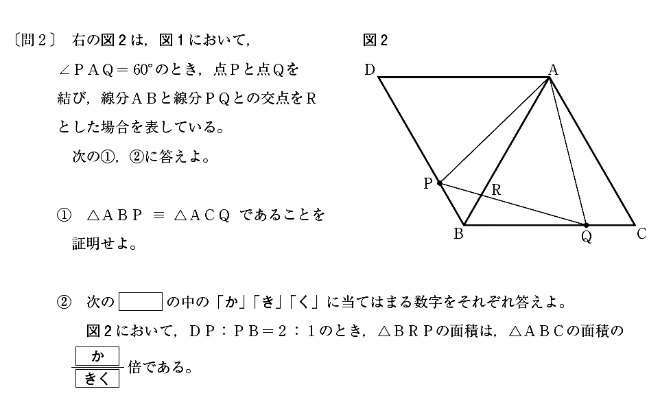
[問2]①は△ABPと△ACQが合同であることを証明する問題です。
それぞれの三角形を見比べて、同じ長さの辺や同じ大きさの角に印をつけていきます。
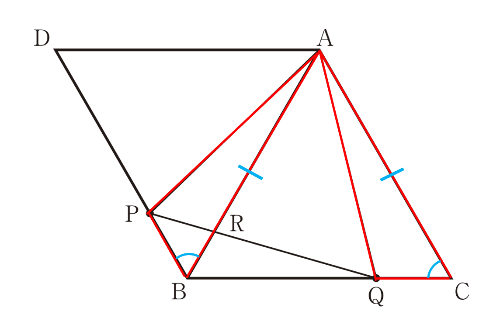
△ABCと△ABDはともに正三角形とわかっているので、AB=ACと∠ABP=∠ACQもすぐに気づくでしょう。ここまで書かれているだけでも部分点をもらえるはずなので、記述式の証明問題を白紙にしてはいけません。
印をつけた図を見ながら、どの合同条件を使えるかを考えます。
もし「2組の辺とその間の角がそれぞれ等しい」を使うなら、BP=CQになるはずです。しかし、BP=CQをどう説明すればよいのかわかりません。
そこで「1組の辺とその両端の角がそれぞれ等しい」を使うことにすると、以下の模範解答のように∠BAP=∠CAQを説明することになります。
△ABPと△ACQにおいて、
仮定から、△ABCと△ABDはともに正三角形だから、
AB=AC … (1)
∠ABP=∠ACQ … (2)
仮定から、 ∠ PAQ=60°
∠BAP=∠PAQ-∠BAQ=60°-∠BAQ
△ABCは正三角形だから∠BAC=60°
∠CAQ=∠BAC-∠BAQ=60°-∠BAQ
よって、∠BAP=∠CAQ … (3)
(1)、(2)、(3)より、1組の辺とその両端の角がそれぞれ等しいから、
△ABP≡△ACQ
相似比と底辺比を利用して面積比を求める問題
[問2]②は面積比を求める問題です。
まずは、△BRPの面積を考えるため、△BRPを含む三角形を探して△BAPを見つけます。
高さの等しい△DAPと△BAPの面積比は底辺比DP:PBに等しく2:1です。したがって、△BAP=\(\frac{1}{3}\)△ABD=\(\frac{1}{3}\)△ABCです。
次に、△BRPが△BAPの何倍かを考えます。AR:RBの比がわかればよいので、ARとRBをそれぞれ一辺とする三角形で相似を探しますが、見つかりません。
ここで△BAD∽△BSPとなるように、Pを通ってBCに平行な線分PSを引きます。
DP:PB=2:1より、正三角形である△SBPの他の2辺PS、SBの比も1です。したがって、AS:SB=2:1より、△BSP=\(\frac{1}{3}\)△BAPです。
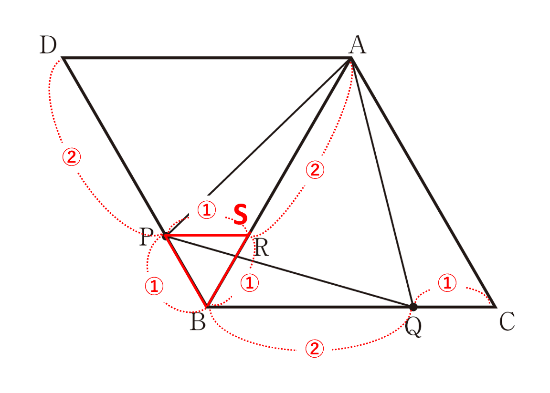
また、BCとPSが平行で、平行線の錯角より∠BQR=∠SPR、∠QBR=PSRとなり、2組の角がそれぞれ等しいから△BQR∽△SPRです。相似比はBQ:SP=2:1=BR:SRとわかります。
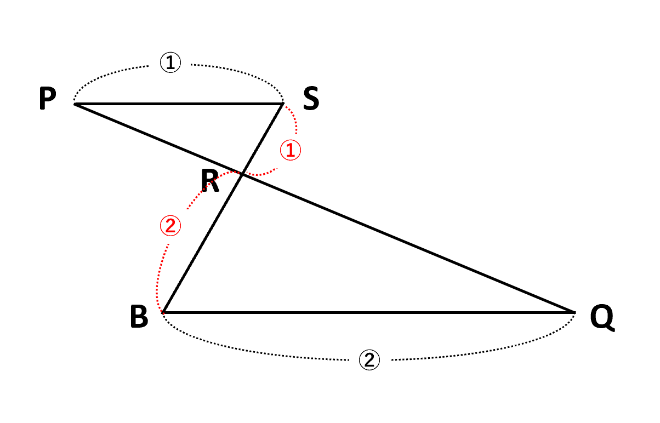
したがって、△BRP=\(\frac{2}{3}\)△BSP=\(\frac{2}{3}\)×\(\frac{1}{3}\)△BAP=\(\frac{2}{3}\)×\(\frac{1}{3}\)×\(\frac{1}{3}\)△ABC=\(\frac{2}{27}\)△ABCとなり、\(\underline{\frac{2}{27}}\)倍が答えです。
【別解】辺を延長する解き方
ここで四角形ACBDが、2つの正三角形をつなげたひし形であることから、ACとDBが平行であることに着目しましょう。
ACをCの方向に、PQをQの方向にそれぞれ伸ばした半直線の交点をSとすると、平行線の錯角より∠RPB=∠RSA、∠RBP=∠RASとなり、2組の角がそれぞれ等しいから△BRP∽△ARSです。
Sと、それぞれの辺の比を書き込んだのが以下の図です。
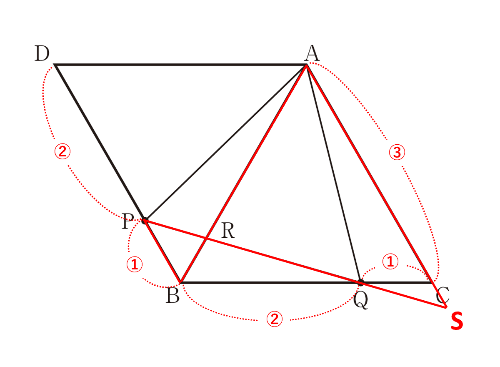
△ABCと△ABDは合同な正三角形なのでBC=BD、[問2]①より△ABP≡△ACQなのでPB=QCです。したがって、BQ:QC=DP:PC=2:1です。また、AC=DBなので、ACの比は3とわかります。
しかし、CSの比がわからないため、△BRPと△ARSの相似比もわかりません。
そこで、ACとDBが平行であることにもう一度着目して、平行線の錯角より∠PBQ=∠SCQ、∠BPQ=∠CSQとなり、2組の角がそれぞれ等しいから△PBQ∽△SCQであることに気づきましょう。
△PBQと△SCQの相似比はBQ:CQ=PB:SC=2:1なので、SC=\(\frac{1}{2}\)PBからSCの比は\(\frac{1}{2}\)です。
△BRPと△ARSに戻って、BP:AS=1:(3+\(\frac{1}{2}\))=1:\(\frac{7}{2}\)=2:7=BR:ARです。
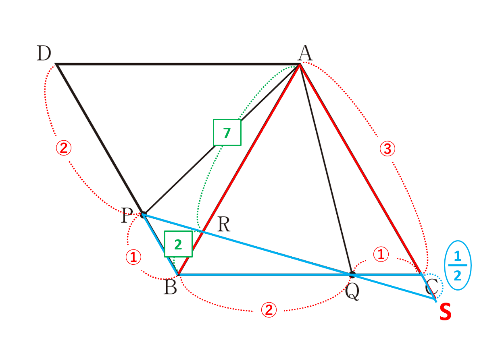
高さの等しい△BRPと△ARPの面積比は底辺比BR:ARに等しく2:7なので、△BRP=\(\frac{2}{9}\)△BAPです。△BAP=\(\frac{1}{3}\)△ABCを代入して△BRP=\(\frac{2}{9}\)×\(\frac{1}{3}\)△ABC=\(\frac{2}{27}\)△ABCとなり、\(\underline{\frac{2}{27}}\)倍が答えです。
正三角形やひし形の性質を利用しないと解けない
令和4年度の大問4は、正三角形を2つつなげたひし形に関する問題でした。そのため、正三角形やひし形の性質を利用しないと問題を解けなかったはずです。
都教委が公表している正答率は、[問1]が62.2%、[問2]①が55.0%、[問2]②が2.3%です。[問1]と[問2]①の正答率があまり高くなかったのは、特殊な図形に慣れていない受験生が少なくなかったからだと考えられます。また、[問2]②は毎年難しいので、よほど数学が得意な受験生以外は捨て問扱いで構いません。
過去10年の都立高校入試問題を徹底分析して分野別にまとめた問題集「高校入試 虎の巻![]() 」で大問4の出題傾向を確認し、[問2]②まで解けるようにしておくとよいでしょう。
」で大問4の出題傾向を確認し、[問2]②まで解けるようにしておくとよいでしょう。
トップ画像=Pixabay



コメント