三角形の面積比に関する問題を解説します。相似比と底辺比を組み合わせて考えましょう。
相似比と底辺比から面積比を求める
【例題】下の図において、三角形ABEと三角形CDEの面積比を求めなさい。ただし、点EはBD上にあるものとします。
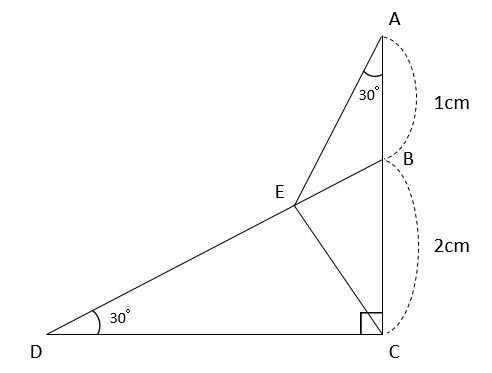
面積比を求める問題では、基準となる三角形の面積を求めて、他の三角形の面積が何倍になるかを考えるのがポイントです。基準となる三角形の面積を具体的に求められない場合は1にしてしまいます。
わかる情報を書き込む
【例題】では、どの三角形を基準にすればいいのかを決めるのが難しいと思います。こういう場合は、わかる情報をどんどん書き込んでいきましょう。わかり情報は角度です。
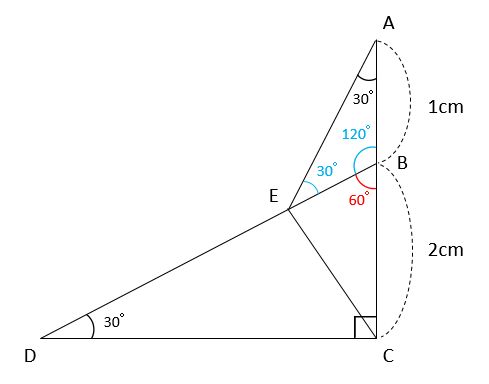
三角形BCDにおいて、三角形の内角の和が180°で、角D=30°、角C=90°だから、角DBC=180°-(30°+90°)=60°です。したがって、角ABE=180°-60°=120°だとわかりました。

三角形BCDは、正三角形を真っ二つにした三角形だよ。三角定規の直角二等辺三角形でない方だね。この形の三角形を見つけたら、問題を解くための手がかりになることが多いよ。
また、三角形ABEにおいて、三角形の内角の和が180°で、角EAB=30°、角ABE=120°なので、角AEB=180°-(30°+120°)=30°です。したがって、三角形ABEは、角EAB=角AEB=30°の二等辺三角形であるとわかりました。
相似比から面積比を求める
三角形ABEのような120°のある二等辺三角形は、正三角形を真っ二つにした三角形に分けられます。下の図のように、BからAEに垂直な補助線を引きましょう。
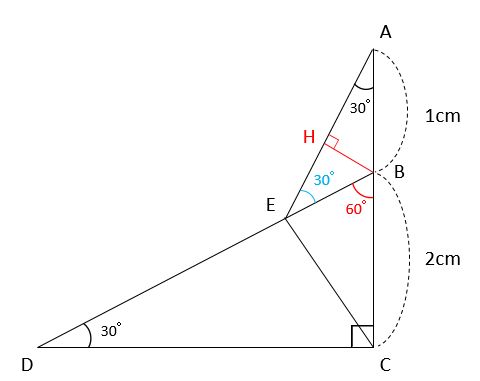

三角形ABEを三角形BHAと三角形BHEに分けたら、三角形BCDと相似な三角形になったわ!相似条件は「2組の角がそれぞれ等しい」ね。

三角形BCDと三角形BHAを、向きをそろえて抜き書きしてみましょう。
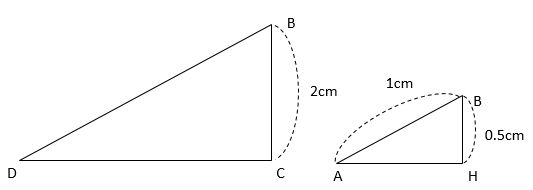
相似な三角形の面積比は相似比×相似比です。
三角形BCDと三角形BHAの相似比は、BC:BH=2:0.5=4:1なので、面積比は2×2:1×1=16:1になります。
面積比で1に当たる三角形BHAを基準にすると、三角形BHAの面積が1であるのに対して三角形BCDの面積は16です。

正三角形を真っ二つにした三角形では、辺の比の2:1を利用します。三角形BCDでは、BD:BC=2:1なのでBD=4cmです。三角形BHAでは、BA:BH=2:1なのでBH=0.5cmです。上ではBHを使いましたが、BD:BA=4:1を使っても同じ結果になります。
底辺比から面積比を求める
三角形BHAと三角形BHEは合同なので、三角形BHEの面積は1です。また、三角形ABE=三角形BHA+三角形BHEより、三角形ABEの面積は2です。
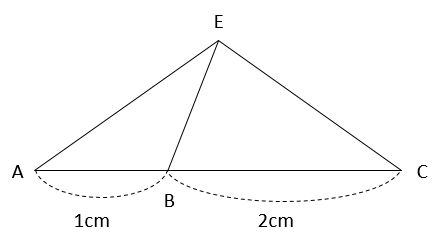
高さが共通する三角形は、底辺比=面積比になります。

三角形ABEと三角形CBEは高さが共通なので、底辺比のAB:CB=1:2が面積比になります。したがって、三角形ABEの面積は2なので、三角形CBEの面積は4です。また、三角形CDE=三角形BCD-三角形CBE=16-4=12です。
以上より、三角形ABEと三角形CDEの面積比は2:12=1:6です。



コメント