問題演習コーナー
この問題のように、もとにする量やくらべる量などを求めていく割合の問題を相当算といいます。
相当算も線分図を描くとわかりやすくなります。
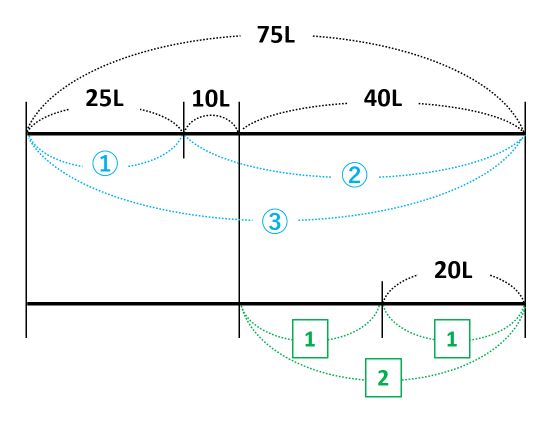
問題文から読み取れる数を書き込んだ線分図は次の通りです。線の上に水の体積、下に割合を書きました。
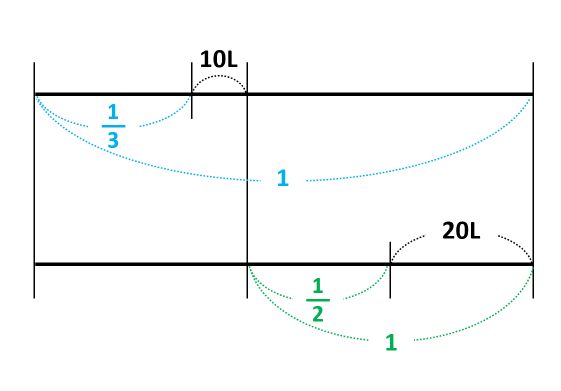
問題文には、\(\frac{1}{3}\)と\(\frac{1}{2}\)の2つの割合があります。
\(\frac{1}{3}\)の「の」の前を見ると、「全体」がもとにする量だとわかります。そのため、\(\frac{1}{3}\)に対応する1は線全体です。
一方、\(\frac{1}{2}\)の「の」の前を見ると、「残り」がもとにする量です。そのため、\(\frac{1}{2}\)に対応する1は、全体の\(\frac{1}{3}\)より10L多く水を出した後の水の量を表す線です。
\(\frac{1}{3}\)と\(\frac{1}{2}\)では、もとにする量が違っているので注意しましょう。
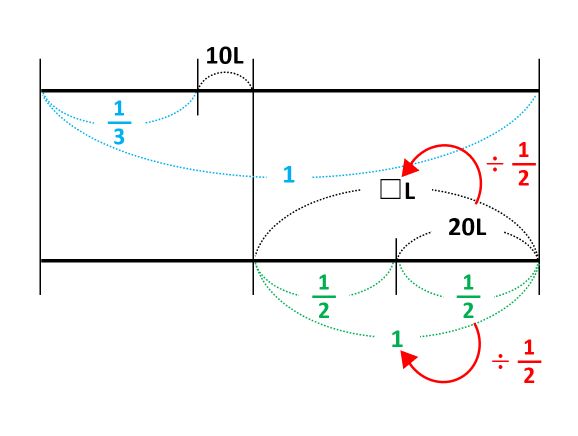
下の線の20Lの下に1-\(\frac{1}{2}\)=\(\frac{1}{2}\)を、1の上に□Lを書き足します。
20Lにかけ算か割り算をすれば□Lを求められると見当をつけて、上と下に並んだ数を見比べます。
下に並んだ数は、右(\(\frac{1}{2}\))から左(1)に÷\(\frac{1}{2}\)なので、上に並んだ数にも同じことをして□=20÷\(\frac{1}{2}\)=40です。
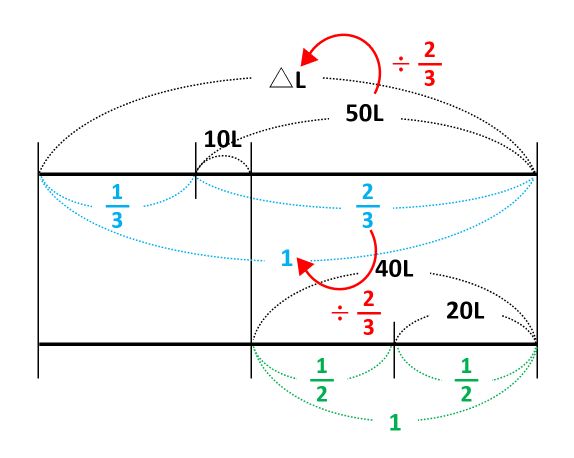
□=40とわかったので、上の線に10+40=50(L)と1-\(\frac{1}{3}\)=\(\frac{2}{3}\)を書き足します。
50Lにかけ算か割り算をすれば△Lを求められると見当をつけて、上と下に並んだ数を見比べます。
下に並んだ数は、右(\(\frac{2}{3}\))から左(1)に÷\(\frac{2}{3}\)なので、上に並んだ数にも同じことをして△=50÷\(\frac{2}{3}\)=75です。これがはじめに入っていた水の量なので、答は75Lです。
別解
割合の計算には分数が入ってくるので、分数計算が苦手だと少し大変です。このような問題は、比を使うと解きやすくなります。
実際に、割合の代わりに比を書き込んだ線分図は次の通りです。
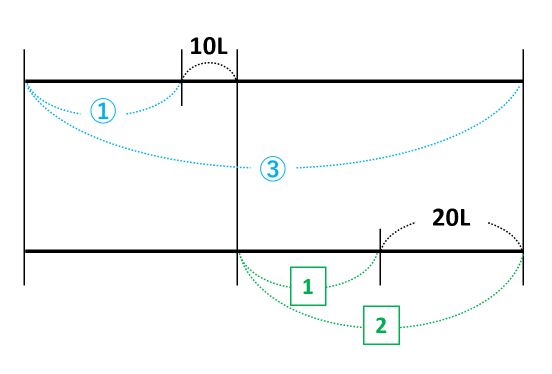
\(\frac{1}{3}\)は1:3、\(\frac{1}{2}\)は1:2と表せます。上の線の比と下の線の比は、もとにする量が違うので、○と□で区別しました。
1=20Lなので、2=40Lとわかります。この40Lに10Lを加えた50Lが②なので、①=25Lです。したがって、はじめに入っていた水の量は③=50+25=75(L)となります。
① 割合はどのようなことを表しますか。
(例)基準となる数を1(倍)としたとき、他の数がどのくらいになるのかを表すことです。
② もとにする量とは何ですか。
(例)基準となる数です。
③ 百分率や歩合とは何ですか。
(例)百分率はもとにする量を100%とする割合で、歩合はもとにする量を10割とする割合です。
トップ画像=Pixabay

コメント