容器と水量に関する問題が中学受験算数ではよく出ます。本記事では、受験生が苦手としやすい問題を解説します。
おもりの一部が水面上に出る?完全に水中に沈む?
容器と水量に関する問題では、おもりを入れる前の水の体積とおもりを入れた後の水の体積は等しいことを利用します。また、水が容器からあふれる場合は、あふれた水の体積も考えます。
【例題】のように、もともとの水面よりもおもりの高さが高いときは場合分けしましょう。なぜなら、下の図からもわかる通り、おもりの一部が水面上に出る場合と、おもりが完全に水中に沈む場合が考えられるからです。
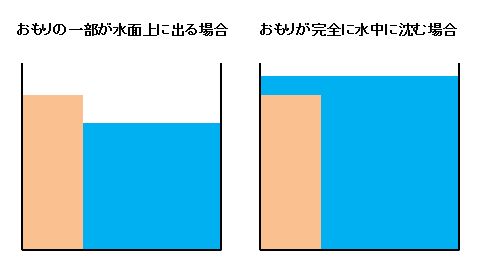
問題文からどちらの場合になるかを決められないときは、どちらかの場合を仮定して問題を解き進めます。答がおかしければ仮定が間違っていたことになりますので、そのときはもう一方の場合を考えます。
おもりの一部が水面上に出る場合
【例題】は場合分けが必要です。まずは、「おもりの一部が水面上に出る」と仮定して問題を解きましょう。
容器と水量に関する問題を解くときは、容器やおもりを立体的に考えるのではなく、平面に置きかえて考えます。その際、横の長さには底面積を書き込むとよいでしょう。
おもりの一部が水面上に出ている図を描くと次の通りです。
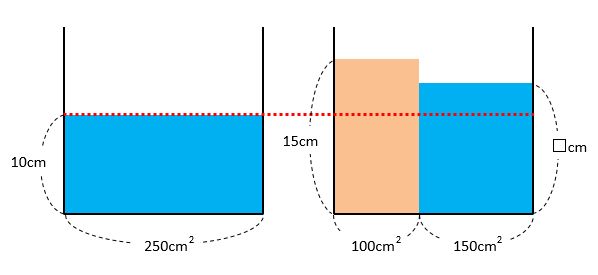
水の量は変わらないことを利用して、次のように式を作って□を求めます。
150×□=250×10
□=2500÷150=\(\frac{50}{3}\)(cm)
答の\(\frac{50}{3}\)(=16.66…)は、おもりの高さである15よりも大きい値です。したがって、「おもりの一部が水面上に出る」という仮定に反するので、おもりが完全に水中に沈む場合を改めて考えます。
おもりが完全に水中に沈む場合
おもりが完全に水中に沈んでいる図を描くと次の通りです。
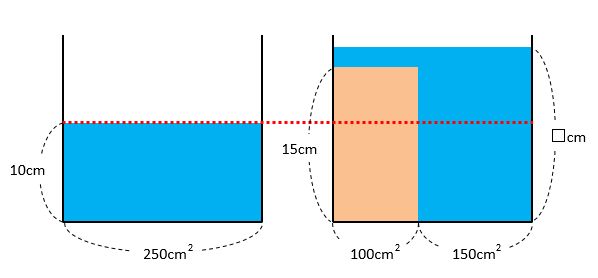
このとき、□を求める方法は次の2通りあります。
「水+おもり」の体積を考える
間違いにくいのは、「水+おもり」の体積を考える方法です。
水の体積は、おもりの入っていない図から、250×10=2500(cm2)。おもりの体積は、100×15=1500(cm2)です。したがって、次のように式を作って□を求めます。
250×□=2500+1500
□=4000÷250=16(cm)
「見かけ上増えた水の体積=おもりの体積」を利用する
たとえば、容器に入った水に石を沈めると、水の体積が増えたように見えます。このとき、見かけ上増えた水の体積は、沈めた石の体積と等しくなります。
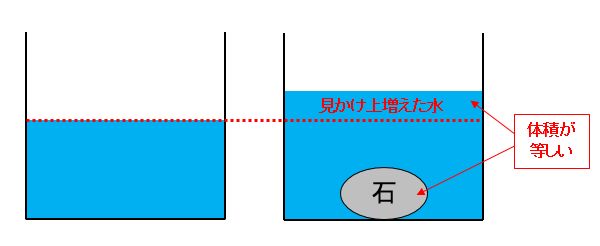
【例題】でも「見かけ上増えた水の体積=おもりの体積」を利用します。
ただし、もともとの水面から出ているおもりの一部にまどわされてはいけません。まどわされないためには、下の図のようにおもりを書きかえるとよいでしょう。
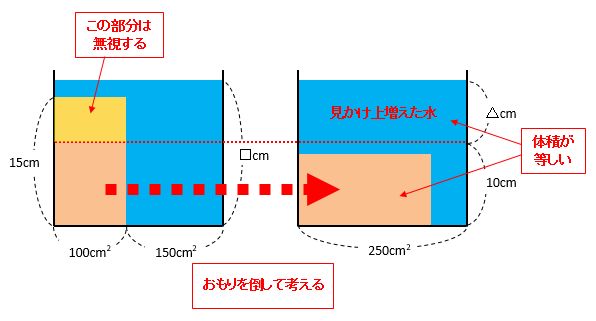
次のように式を作って△を求めます。
△×250=1500
△=1500÷250=6
□=6+10=16(cm)
場合の数の場合分けと容器と水量の場合分けは違う
場合の数の問題では、「一の位が0の場合」と「一の位が0以外の場合」のように場合分けすることが少なくありません。このような場合分けと、容器と水量の問題を解くときの場合分けは、ちょっと違います。
場合の数の場合分けは、すべての場合で答えを求めて、それらを足すことで最終的な答えになります。つまり、すべての場合を考えなければ正解になりません。
一方、容器と水量に関する問題の場合分けは、両立しない場合の一方を考えて、その答がおかしければ他方を考えます。したがって、一方の場合でおかしくない答を求められれば、他方を考える必要はありません。
こうした違いも理解して、容器と水量に関する問題でも場合分けを意識することが大切です。
トップ画像=Pixabay




コメント
分かりやすい、説明ありがとうございます。
一点だけ、確認したく思いますが、「実際に、おもりの一部が水面上に出る状態で、冒頭の問題の絵を描きます。」の下に掲載されている図は完全に沈んだ図が配置されているようですが…
山谷様
ご指摘ありがとうございます。
私の方のミスで挿入すべき図を誤っていたため、修正いたしました。
また何かありましたら、ご遠慮なくご指摘くださいませ。
今後ともどうぞよろしくお願いいたします。
みみずく
みみずく様
早速、ご確認をいただき、ありがとうございました。
分かりやすいご説明を、今後とも、子供の勉強の参考にさせていただきます。
山谷
山谷様
こちらこそ、ありがとうございました。
記事がお役に立つのでしたら、とても嬉しいことです。
お子さんのお勉強が捗ることを願っております。
みみずく
これは知りたいことじゃなかった。内法の縦と横の長さがわかってる直方体の容器に◯dL入れたら深さは何cmになるかという問題の深さの求め方を知りたかった。
これは塾で習った。
でも、詳しく説明していいと思った。
どうもありがとう。
これからもがんばって。 私も頑張る。
よろタンバリンシャンシャン