都立高校入試の令和4年度の過去問から、数学の大問3(グラフと図形)を解説します。
bのとる値の範囲を求める問題
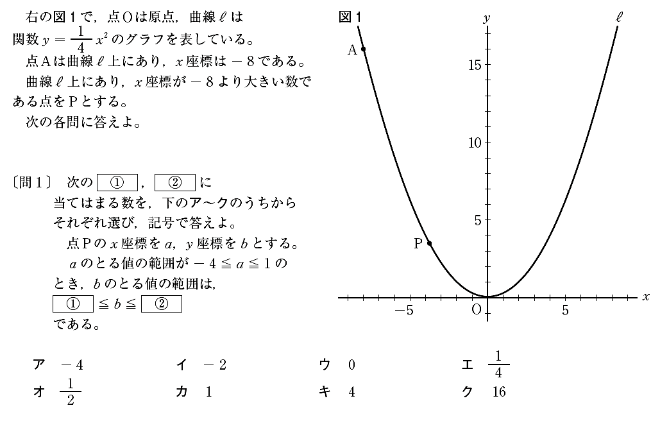
[問1]は、Pの座標(a、b)の範囲を求める問題です。変域と同じ考え方をします。
aのとる値の範囲が-4≦a≦1なので、この範囲でbがy=\(\frac{1}{4}\)x2のグラフ上を動きます。
下の図から、bの値が一番小さくなるのは、青い矢印の一番下になるy=0のときです。一方、bの値が一番大きくなるのは、青い矢印の一番上になるy=\(\frac{1}{4}\)×(-4)2=4のときです。したがって、0≦b≦4となって、①がウ、②がキです。
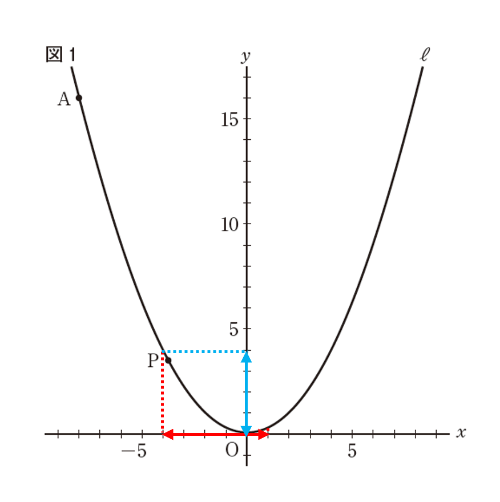
ちなみに、y=\(\frac{1}{4}\)x2に-4≦a≦1の両端の値を代入して、\(\frac{1}{4}\)≦a≦4とすると間違いです。1よりも小さい0がbのとる範囲に含まれることに注意しましょう。
2点を通る直線の式を求める問題
[問2]は、2点A、Pを通る直線の式を求める問題です。
まずは、A、Pの座標を求めましょう。
Aはy=\(\frac{1}{4}\)x2上の点で、x座標が-8です。したがって、x=-8をy=\(\frac{1}{4}\)x2に代入してy=\(\frac{1}{4}\)×(-8)2=16なので、A(-8、16)です。
同様に、Pもy=\(\frac{1}{4}\)x2上の点で、x座標が2なので、y=\(\frac{1}{4}\)×22=1よりP(2、1)です。
次に、y=ax+bにA(-8、16)とP(2、1)の値をそれぞれ代入して、16=-8a+b、1=2a+bです。この2つの式を連立して解くとa=-\(\frac{3}{2}\)、b=4となるので、③がア、④がエです。
Pのx座標を求める問題
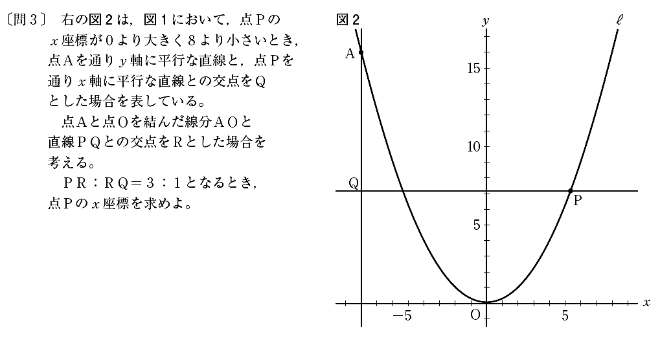
[問3]は、Pのx座標を求める問題です。
解き方は相変わらずワンパターンで、以下の記事の手順通りです。

まずは、未知の点Pのx座標([問3]の答えとなるx座標)をtとおきます。
次に、P、Q、Rの座標をtを使って表します。
Pはy=\(\frac{1}{4}\)x2上の点で、x座標がtなので、y=\(\frac{1}{4}\)t2よりP(t、\(\frac{1}{4}\)t2)です。
AQはy軸に平行なので、Qのx座標はAのx座標と同じで-8です。また、PQはx軸に平行なので、Qのy座標はPのy座標と同じで\(\frac{1}{4}\)t2です。したがって、Q(-8、\(\frac{1}{4}\)t2)です。
Rの座標を求めるには、先に線分AOの式を求める必要があります。線分AOは原点を通り、傾きは\(\frac{16}{-8}\)=-2なので、式はy=-2xです。また、ARはx軸に平行なので、Rのy座標はPのy座標と同じで\(\frac{1}{4}\)t2です。したがって、y=-2xにy=\(\frac{1}{4}\)t2を代入して、x=-\(\frac{1}{8}\)t2となりR(-\(\frac{1}{8}\)t2、\(\frac{1}{4}\)t2)です。
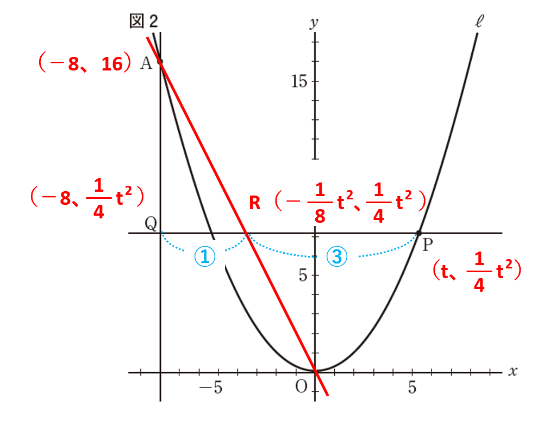
最後に、PRとRQをtで表して、PR:RQ=3:1をtの式で表して計算します。
PR=t-(-\(\frac{1}{8}\)t2)=t+\(\frac{1}{8}\)t2
RQ=-\(\frac{1}{8}\)t2-(-8)=-\(\frac{1}{8}\)t2+8より、
(t+\(\frac{1}{8}\)t2):(-\(\frac{1}{8}\)t2+8)=3:1
t+\(\frac{1}{8}\)t2=3(-\(\frac{1}{8}\)t2+8)
t+\(\frac{1}{8}\)t2=-\(\frac{3}{8}\)t2+24
両辺に8をかけて、
8t+t2=-3t2+192
4t2+8t-192=0
両辺を4で割って、
t2+2t-48=0
(t+8)(t-6)=0
0<t<8よりt=6([問3の答え])
グラフと図形の問題は全問正解を狙える
大問3は例年通り、何のひねりもない簡単な問題でした。
都教委が公表している正答率は、[問1]が67.7%、[問2]が69.4%、[問3]が14.7%です。[問1]と[問2]で失点すると、他の受験生と差がついてしまいます。一方、[問3]は簡単であるにもかかわらず、正答率は15%を切っています。Rのx座標を求められなかった受験生が多いのかもしれません。
グラフと図形の問題は解法がワンパターンで計算量も少ないサービス問題です。過去10年の都立高校入試問題を徹底分析して分野別にまとめた問題集「高校入試 虎の巻![]() 」でしっかり練習して、本番でも全問正解を狙いたいところです。
」でしっかり練習して、本番でも全問正解を狙いたいところです。
トップ画像=Pixabay



コメント