【速さと比】歩数と歩幅の問題が苦手？線分図を描けばわかりやすいよ

中学受験算数の「速さと比」の単元には、歩数と歩幅の問題があります。「太郎君が4歩で歩く道のりを次郎君は5歩で歩き……」のような問題です。

多くの受験生はこのタイプの問題を苦手とします。問題集などの解説でいきなり歩幅を求める計算が始まるからです。

今回は、歩数と歩幅の問題を線分図を描きながらわかりやすく解説します。

オカルト進学塾

志望校合格とオカルトエリートを目指す受験勉強サイト

occult-shingakujuku.com

一定のものを探そう

次の【例題】を考えてみましょう。

歩数と歩幅の問題では、最初に道のり・速さ・時間のうち、一定のものを探すことが大切です。

1文目は、「、」の前後で一定のものが変わります。

「太郎君が4歩で歩く道のりを次郎君は5歩で歩き、」では、2人が歩く道のりが一定です。一方、「太郎君が4歩歩く間に次郎君は3歩歩きます。」では、2人が歩く時間が一定です。

わかることを線分図に表そう

一定のものを見つけた後は、わかることを線分図に表します。

1文目の「、」の前が【図1】で、「、」の後が【図2】です。線分図の長さは道のりを表します。

線分図から歩幅を求めよう

【例題】で求めるべきものは、速さの比です。

比を求めるので、2つの線分図を見ながら、次の関係を利用することを考えます。

【図1】は、道のりが一定なので、時間の比を求められれば速さの比も求められます。しかし、【図1】や【図2】から時間の値（比）を求めるのは難しいと思います（逆比を使うため）。

そこで、【図2】に注目します。こちらは、時間が一定なので、道のりの比（＝線分の長さの比）がそのまま速さの比になります。ここで必要となるのは、太郎君と次郎君の歩幅（一歩で進む道のり）です。なぜなら、「歩幅×歩数＝歩いた道のり」だからです。

エノキさん

歩幅が60cmの人が10歩歩けば、60×10＝600cm（6m）の道のりを歩いたことになるのね！

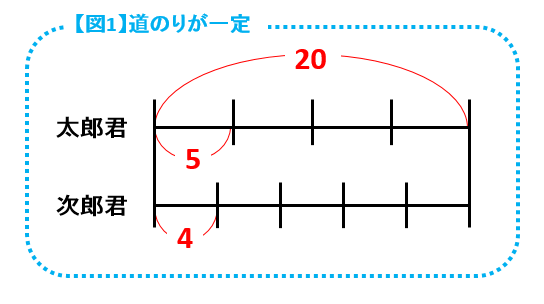
もう一度【図1】を見ましょう。こちらは、道のりが一定なので、太郎君と次郎君の歩幅を求められます。ただし、道のりがわかっていないので、自分で道のりを決めてしまうのがポイントです。

たとえば、【図1】の道のり（線分全体の長さ）を太郎君と次郎君の歩数の最小公倍数である20にすると、太郎君の歩幅は20÷4＝5、次郎君の歩幅は20÷5＝4となります。

シイタケくん

道のり（線分全体の長さ）は好きな数字にしていいんですか？

エリンギ先生

どんな数字でも構わないよ。

エノキさん

問題集の解説では、道のりが1になっていることが多いんですが……

エリンギ先生

道のりを1にしてもいいんだけど、歩幅が分数になって、わかりにくくなるよ。

求めた歩幅と【図2】から、一定の時間で太郎君が歩いた道のりは5×4＝20、次郎君が歩いた道のりは4×3＝12です。

時間が一定のとき、道のりの比＝速さの比なので、太郎君の速さ：次郎君の速さ＝太郎君が歩いた道のり：次郎君が歩いた道のり＝20：12＝5：3です。

いきなり計算するのはやめよう

歩数と歩幅の問題では、いきなり計算で歩幅を求めようとしても、わからなくなってしまいます。一定のものを探して、線分図などにわかることを表してみることが大切です。