中学受験算数の整数問題の中から、多くの中学受験生が苦手とする難問を解説します。割り算や素因数分解などの知識を活かしましょう。
整数の積は2で何回割り切れるか?
【例題1】は、Aが積(かけ算)であることを利用して、2で割り切れる回数を求めます。ここで大切なのは「『割り切れる』とはどういうことか?」です。
「2で割り切れる」とはどういうことか?
6÷2は商が3であまりが0です。このようにあまりが0になることを「割り切れる」といいます。しかし、「あまりが0になる=割り切れる」だけだと、【例題1】は解けません。
もう一度6÷2の6を見てみましょう。6を素因数分解(素数の積で表すこと)すると6=2×3です。同じように、2で割り切れる数を素因数分解すると、8=2×2×2(2×4)、14=2×7(2×7)、20=2×2×5(2×10)となります。2で割り切れる整数はすべて「2×整数」の形をしていることがわかるでしょう。
このことから、整数Nが整数mで割り切れるとき、N=m×n(nは整数)が成り立ちます。小学算数だと、Nを「割られる数」、mを「割る数」、nを「商」と習うので、「割られる数=割る数×商」と表せます。

2で割り切れる整数は2の倍数になっているよ!

2が約数になっている整数が2で割り切れるとも考えられるわ!

シイタケくんやエノキさんの考えは正しい。割り算を倍数や約数と結び付けて理解しておくのは大事だよ。

「2で2回割り切れる」とはどういうことか?
12÷2=6→6÷2=3なので、12は2で2回割り切れます。12=2×2×3となり、×2が2個ある整数は2で2回割り切れるとわかります。同じように、24=2×2×2×3は×2が3個あるから、2で3回割り切れます。80=2×2×2×2×5は×2が4個あるから、2で4回割り切れます。
【例題1】では「Aは2で何回割り切れますか」と問われているので、Aに×2が何個あるかがわかればよいと考えられます。
小さい数字で具体的に考える
Aに×2が何個あるかを調べるには、「×2の個数をどうやって数えるか?」も考えなければなりません。
【例題1】の前に、A=1×2×3×4×5×6×7×8×9×10という小さい数字で具体的に考えましょう。Aの2、4、6、8、10に×2があります。つまり、1から10までの整数の中にある2の倍数の個数分だけ×2があります。したがって、×2は10÷2=5(個)あります。
しかし、これで終わりにしてはいけません。4=2×2や8=2×2×2はそれぞれ×2が1個だけではないからです。つまり、2の倍数の個数(10÷2=5)に4の倍数の個数(10÷4=2)と8の倍数の個数(10÷8=1)を加えた8個が×2の個数です。
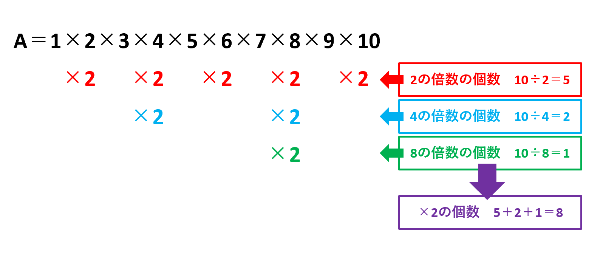
A=1×2×3×4×5×6×7×8×9×10にある×2の個数は「(1から10までの整数の中にある)2の倍数の個数+4の倍数の個数+8の倍数の個数」なので、Aは2で8回割り切れます。

10を割った2、4、8は4=2×2、8=4×2なので、2をどんどん2倍していった数だわ。10以下の数を考えるので8までなのね。
Aは2で何回割り切れるか?
【例題1】も、A=1×2×3×4×5×6×7×8×9×10と同じように考えます。
- 2の倍数の個数 … 100÷2=50(個)
- 4の倍数の個数 … 100÷4=25(個)
- 8の倍数の個数 … 100÷8=12(個)
- 16の倍数の個数 … 100÷16=6(個)
- 32の倍数の個数 … 100÷32=3(個)
- 64の倍数の個数 … 100÷64=1(個)
したがって、Aにある×2の個数は50+25+12+6+3+1=97(個)なので、Aは2で97回割り切れます。

【例題1】は「Aは2で何回割り切れますか」だけれど、「Aを2で割り続けるとき、何回目で商が整数でなくなりますか」と聞かれることもあるんだ。商が整数でなくなるのは97回割った後なので、97+1=98(回目)が正解だよ。何を答えるのかをしっかり区別しよう!
整数の積は10で何回割り切れるか?

【例題2】も【例題1】と同じように考えて、100÷10=10、100÷100=1だから10+1=11(回)です!

残念!よくある間違いだね。

えっ?違うんですか?
小さい数字で具体的に考える
【例題2】も、A=1×2×3×4×5×6×7×8×9×10という小さい数字で具体的に考えると理解しやすいでしょう。
A=1×2×3×4×5×6×7×8×9×10は、×10があるので、少なくとも1回は10で割り切れます。しかし、×2と×5から×2×5=×10がもう1つ出てきます。そのため、10で2回割り切れるとわかります。
この2回を計算で求めましょう。10=2×5なので、×2と×5の個数をそれぞれ求めます。×2の個数は「(1から10までの整数の中にある)2の倍数の個数+4の倍数の個数+8の倍数の個数」で8個です。また、×5の個数は10÷5=2(個)です。×5がすべて×2とセットになって×10になるので、×5の個数が×10の個数になります。
したがって、「×10の個数=×5の個数」なので、Aは10で2回割り切れます。

今回は、×2の個数が×5の個数よりも多いから「×10の個数=×5の個数」になりました。問題によっては、×2の個数が×5の個数よりも少なくて、「×10の個数=×2の個数」になることもあります。面倒くさがらずに、×2の個数と×5の個数の両方を求めておいた方がよいでしょう。
Aは10で何回割り切れるか?
【例題2】も、A=1×2×3×4×5×6×7×8×9×10と同じように考えます。
×2の個数は【例題1】から97個です。
×5の個数は、次の計算から20+4=24(個)です。
- 5の倍数の個数 … 100÷5=20(個)
- 25の倍数の個数 … 100÷25=4(個)
×5がすべて×2とセットになって×10になるので、「×10の個数=×5の個数」から、Aは10で24回割り切れます。

【例題2】の「Aは10で何回割り切れますか」は、「Aは一の位から0が連続して何個ならびますか」という問題になることもあるわ。10で割り切れる回数と、一の位から連続してならぶ0の個数は同じなのよ。こういうのも考えてみるとおもしろいわ!



コメント
中3です。勉強になる記事ばかりで目からウロコでした。
早速ですが、3つ質問があります。
心情を読み取るにはどうしたらいいのか?
短い文章だったり心情語が直接かかれている場合はいいのですが複雑な文章や行動から推測する必要がある問題になると頭がごちゃごちゃになります。
素早く言い換える力をつけるには?
語彙力を鍛える必要があると思いますが具体的にどのようにしたら良いのでしょうか。
50字 80字といった長文の記述問題で
構造を理解して、記述を考えて、書くという過程を時間内に出来るのでしょうか?やはり積み重ねですか?
コメントありがとうございます。
以下はご質問への回答です。
> 心情を読み取るにはどうしたらいいのか?
「複雑」のレベルがどのくらいを想定しているのかがわかりませんが、入試に出る小説ならば、心情読み取りはある程度パターン化できます。
たとえば、過去記事にも書きましたが、「顔が赤くなる」ならば「怒り」「恥ずかしさ」「恋愛感情」のどれかです。
こういう行動や表情などと直接的な心情表現を対応させてまとめ、自分なりの「心情ノート」みたいなのを作っておくと便利だと思います。
> 素早く言い換える力をつけるには?
これも「心情ノート」と同じく、自分なりにノートなどにまとめておくと役立ちます。
特に「憤怒=憤り=怒り」のように、音読みの熟語を訓読みに分解してみると語彙を増やしやすいです。
後は「現代文キーワード集」のような参考書を読んでいくとよいと思います。
一問一答形式の単語帳で語彙を増やすのは効果的ではありますが、暗記が苦手だと時間がかかる割に…となりやすいです。
> 50字 80字といった長文の記述問題で構造を理解して、記述を考えて、書くという過程を時間内に出来るのでしょうか?
50~80字だとそれほど長い記述ではありません。
本文中の根拠を精々2~3つ見つけてまとめるだけなので、それほど苦労しないと思います。
基本的には抜き出し問題の延長と考えて、本文中の根拠に線を引き、不要な部分を削り、論理関係だけ注意して記述します。
自分の頭で考える要素はほとんどありませんので、慣れればただの作業で、それなりに速くできるようになります。
中3だと受験勉強の真っただ中ですね。
日々の受験勉強を意味のあるものにしてほしいと思います。
応援しています!
ありがとうございます。
いつも記述問題でどうやって書こうか悩んで時間オーバーになってしまいます。たくさん問題を解いていったら良いのでしょうか?
特に小説の記述問題では
①何となく分かるが文章をまとめられない!
②内容は合っているがキーワードが入っておらず不正解
③根拠っぽい箇所を見つけたのはいいが複数あって迷う
これらを改善するにはどうしたら良いでしょうか。
ご質問への回答です。
> いつも記述問題でどうやって書こうか悩んで時間オーバーになってしまいます。
そもそもの話として、書き方で悩んではいけません。
小説ならば「感情が起こった原因or感情が向かう対象+直接的な感情表現」でまとめるだけです。
たとえば、「花瓶を壊して母に叱られたことで落ち込む気持ち。」「花子にラブレターを渡せるかどうかを不安がる気持ち。」などです。
さらに、字数に合わせて、感情が起こった原因or感情が向かう対象を詳しく書きます。
「花瓶を壊して~」ならば「なぜ花瓶を壊したのか?」「母にどのように叱られたのか?」などを膨らませます。
このように型を決めて書くことが大切です。
> ①何となく分かるが文章をまとめられない!
ここまででお伝えした通りです。
> ②内容は合っているがキーワードが入っておらず不正解
キーワードが入っていないということは、そもそも内容が合っていないと思われます。
まずは最低限必要となる言葉を決めて、それらを詳しく説明していくのがコツです。
「花瓶を壊した」「母に叱られた」「落ち込む」という解答の骨格となる言葉を抽出する訓練をしてみてください。
> ③根拠っぽい箇所を見つけたのはいいが複数あって迷う
根拠っぽいではダメで、確実に「ここが根拠だ!」と言える箇所を特定してください。
その特定のためのテクニックを磨く必要があります。
たとえば、傍線部の言いかえならば、傍線部中の指示語や抽象的な言葉の説明になっている箇所が根拠です。
それらを探すためには、指示語や接続をヒントにしたり、同じ(似た)言葉を探したりします。
まずは、抜き出し問題でほぼ100%正解できるように練習するとよいと思います。
> たくさん問題を解いていったら良いのでしょうか?
志望校の過去問を中心として、正解に至る方法を自分なりに確立してください。
具体的には、正解を見た後、本文中のどこに根拠があり、どういう手順でその根拠にたどり着けるのかを自分なりに考えます。
解説を読む前に正解から逆算することです。
逆算して「こういう手順でここに根拠がある」と分かった後、解説と自分の考えが合致するかどうかを確認します。
ただ、高校入試用の問題集だと、解説がダメなものも多いので要注意です。
たくさん問題を解くのではなく、正解から逆算する訓練をしばらく続けてみてください。
ありがとうございました。頑張ります。