【場合の数】樹形図や計算で順列を考える！Pや階乗の公式も簡単だよ

問題演習コーナー

【問題】男子4人、女子3人の中から3人のリレー選手を選びます。走る順番まで決めるとして、次の問いに答えましょう。

(1) 男女7人から選ぶとき、選び方は何通りありますか。

(2) 男子から2人、女子から1人を選ぶとき、選び方は何通りありますか。

(3) 女子が少なくとも1人入っている選び方は何通りありますか。

7人もいるので樹形図を描くと大変です。計算で答を求めましょう。

ちなみに、人間を選ぶ場合、一人一人を異なるものと考えます。一方、「赤玉4つ、白玉3つとの中から3つを選ぶ」という場合、4つの赤玉と3つの白玉をそれぞれ同じものと考えます。人間と物とでは扱い方が違うので要注意です。

7人から3人を選んで並べるので、7×6×5＝210（通り）が答です。

男子の選び方は、男子4人から2人を選んで並べるので4×3＝12（通り）です。

女子の選び方は、3人から1人を選ぶので3通りです。

男子を●、女子を○とすると、男子と女子の走る順番は●●○、●○●、○●●の3通りです。

積の法則より12×3×3＝108（通り）が答です。

シイタケくん

男子と女子の走る順番を考えるのがポイントだね！

① 女子から3人を選ぶとき、女子3人を並べるので3×2×1＝6（通り）です。

② 男子から1人、女子から2人を選ぶときを考えます。

男子の選び方は、4人から1人を選ぶので4通りです。

女子の選び方は、3人から2人を選んで並べるので3×2＝6（通り）です。

男子を●、女子を○とすると、男子と女子の走る順番は●○○、○●○、○○●の3通りです。

積の法則より4×6×3＝72（通り）です。

③ 男子から2人、女子から1人を選ぶとき、(2)より108通りです。

①～③は同時に起こらないので、和の法則より6＋72＋108＝186（通り）が答です。

「女子が1人も入っていない選び方」は、「女子が少なくとも1人入っている選び方」の余事象といいます。この余事象を使うと、「女子が少なくとも1人入っている選び方」＝「すべての選び方」－「女子が1人も入っていない選び方」で求められます。

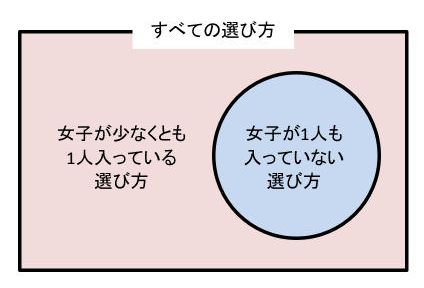
女子が1人も入っていないとき、男子4人から3人を選んで並べるので4×3×2＝24（通り）です。

したがって、女子が少なくとも1人入っている選び方は210－24＝186（通り）です。

① 樹形図を描くとき、どのようなことを意識するとよいですか。

（例）自分なりにルールを決めて規則的に描くことと、縦や横に数字などをそろえることです。

② 積の法則では、どのようなことが成り立ちますか。

（例）事柄AとBについて、（AとBのどちらも起こる場合の数）＝（Aが起こる場合の数）×（Bが起こる場合の数）が成り立ちます。

トップ画像＝Pixabay