サイコロの目の出方やリレー選手の選び方など、ある事柄の起こり方全てを数え上げるのが「場合の数」です。小学算数から大学受験数学まで、ほぼ同じ内容の問題が出題されます。
今回は、そんな場合の数の基本となる「順列」と「組合せ」の区別、「和の法則」と「積の法則」の区別について解説します。
「順列」と「組合せ」を正しく使い分けよう
【例題】1、2、3、4の書かれた4枚のカードがあります。このとき、次の問いに答えましょう。
(1) 4枚の中から2枚を選んで2けたの整数を作るとき、何通りの整数ができますか。
(2) 4枚の中から同時に2枚を取り出すとき、何通りの取り出し方がありますか。
(1)と(2)の違いは何でしょうか?
(1)はカードの並び順を考えますが、(2)は並び順を考えない、という違いがあります。そして、この違いに注目すると、場合の数の問題は「順列」と「組合せ」の2パターンに大きく分けられます。
順列とは、並び順を考える場合の数です。一方、組合せは、並び順を考えない場合の数です。 (1)は順列で (2)は組合せです。
それぞれの違いに気を付けながら、樹形図を描いてみましょう。樹形図とは、全ての場合を枝分かれで描いた図のことです。
並び順を考える場合の数が「順列」
まずは(1)の樹形図です。
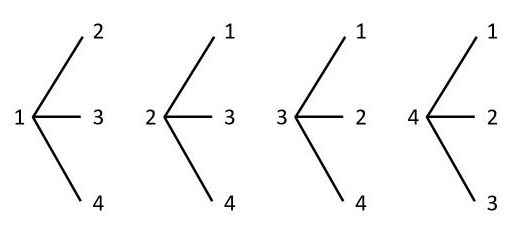
単純に全ての数字を使って樹形図を描きました。その結果、(1)の答は12通りだとわかります。
並び順を考えない場合の数が「組合せ」
(2)の樹形図は(1)とは違います。たとえば、(1)では12と21を区別しますが、(2)では12と21を同じものと考えます。組合せの問題では、同じものを最初から書かないようにするとまちがいを防げます。
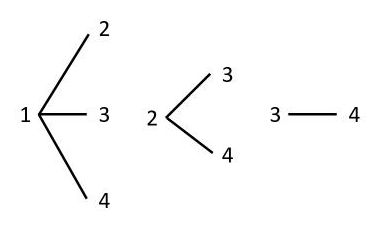
「ある数字の後ろの枝に書くのは、その数字より大きい数字だけ」というルールを決めて樹形図を描きました。その結果、余計な枝が消えて、(2)の答が6通りだとわかりました。

樹形図を数える場合、どこを見て数えればいいんですか?

樹形図は枝分かれの一番右側を数えてね。たとえば、1――2という枝があったら、2の方だけ数えて1通りだ。たまに、1と2の両方を数えて「2通りです」と言う生徒がいるけれど、その数え方はまちがいだよ。
「和の法則」と「積の法則」を正しく使い分けよう
【例題】の(1)を計算で解いてみましょう。このとき、2種類の解き方があります。
どちらかが起こる場合の数は「和の法則」
十の位がどの数字になるかで場合分けします。
① 十の位が1の場合、一の位は2、3、4の3通りです。
② 十の位が2の場合、一の位は1、3、4の3通りです。
③ 十の位が3の場合、一の位は1、2、4の3通りです。
④ 十の位が4の場合、一の位は1、2、3の3通りです。
したがって、①~④より3+3+3+3=12(通り)が答です。
①~④はどれかしか起こりません。たとえば、①と②がどちらも起こると考えると、十の位が1であり2でもある整数ができることになっておかしいとわかります。
このように、事柄AとBについて、(AかBのどちらかが起こる場合の数)=(Aが起こる場合の数)+(Bが起こる場合の数)が成り立ちます。これを和の法則といいます。
どちらも起こる場合の数は「積の法則」
十の位になる可能性のある数字と、一の位になる可能性のある数字をそれぞれ考えます。
① 十の位は1、2、3、4の4通りです。
② 一の位は十の位で使った数字以外の3通りです。
したがって、①と②より4×3=12(通り)が答えです。
①と②の場合の数をかけたのは、十の位が1、2、3、4のそれぞれの場合で一の位は3通りずつあるからです。①と②はどちらも起こらないとそもそも2けたの整数を作れません。
このように、事柄AとBについて、(AとBのどちらも起こる場合の数)=(Aが起こる場合の数)×(Bが起こる場合の数)が成り立ちます。これを積の法則といいます。
場合の数では区別を大切にしよう
たとえば、クラスの30人から2人の学級委員を選ぶ場合、その選び方は組合せです。2人の学級委員は同じ役割なので、(太郎君、花子さん)という選び方と(花子さん、太郎君)という選び方に区別がないからです。
一方、学級委員1人と図書委員1人の計2人を選ぶ場合、その選び方は順列です。(学級委員、図書委員)とすると、(太郎君、花子さん)という選び方と(花子さん、太郎君)という選び方を区別するからです。

クラスの30人から3人のリレー選手を選ぶ場合、組合せでいいんですか?

3人のリレー選手を選ぶだけなら組合せだ。だけど、走る順番まで決めてしまうなら順列になるよ。たとえば、(A君→B君→C君)という順番と(B君→A君→C君)という順番は違うからね。
場合の数の問題では、「順列」と「組合せ」、「和の法則」と「積の法則」をそれぞれ区別することがとても大切です。同じように見える問題でも、「何が違うのかな?」と普段から考えるようにしましょう。
次の質問に答えましょう。(解答例は最後のページにあります)
① 順列と組合せの違いは何ですか。
② 和の法則を使う問題と積の法則を使う問題はどのように区別しますか。





コメント