【場合の数】順列と組合せ、和の法則と積の法則を正しく使い分けよう

問題演習コーナー

【問題】下の図は、A、B、Cの3地点を行き来するときに利用できる交通手段とそれぞれの所要時間を表しています。

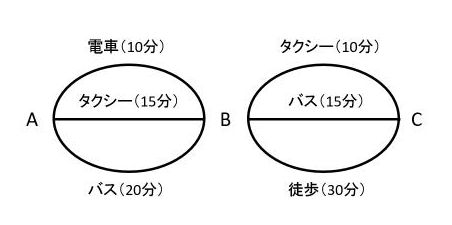
乗り物を利用するときの待ち時間は考えないものとして、次の問いに答えましょう。

(1) AからBを通ってCまで行く方法は、全部で何通りありますか。

以下の問いでは、AからBを通ってCまで行った後、Bを通ってAまで戻ってくることを考えます。

(2) バスを1回だけ利用する方法は、全部で何通りありますか。

(3) Aを出発してから1時間以内でAに戻ってくる方法は、全部で何通りありますか。ただし、Cに着いてからCを出発するまでの時間は考えないものとします。

A→Bの交通手段は3通り、B→Cの交通手段は3通りです。

A→BとB→Cは続けて起こるので、積の法則を使って3×3＝9（通り）が答です。

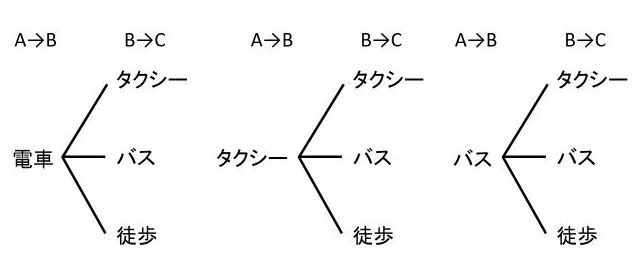
ちなみに、樹形図を描くと以下の通りです。

どこでバスを利用するかで分けて考えます。このように、いくつかの場合を分けることを場合分けといいます。

① A→Bでバスを利用する場合、A→Bは1通り（バス）、B→Cは2通り（バス以外）、C→Bは1通り（バス以外）、B→Aは1通り（バス以外）です。これらは全て続けて起こるので、積の法則より1×2×2×2＝8（通り）です。

② B→Cでバスを利用する場合、A→Bは2通り（バス以外）、B→Cは1通り（バス）、C→Bは1通り（バス以外）、B→Aは1通り（バス以外）です。積の法則より2×1×2×2＝8（通り）です。

③ C→Bでバスを利用する場合、A→Bは2通り（バス以外）、B→Cは2通り（バス以外）、C→Bは1通り（バス）、B→Aは2通り（バス以外）です。積の法則より2×2×1×2＝8（通り）です。

④ B→Aでバスを利用する場合、A→Bは2通り（バス以外）、B→Cは2通り（バス以外）、C→Bは2通り（バス以外）、B→Aは2通り（バス）です。積の法則より2×2×2×1＝8（通り）です。

①～④は同時に起こらないので、和の法則より8＋8＋8＋8＝32（通り）が答です。

① バスを利用する道をA→B、B→C、C→B、B→Aの中から1つ選ぶので4通りです。

② バスを利用する道以外ではバス以外の2種類の交通手段を利用することになります。これらの道を行き来する方法は、積の法則より2×2×2＝8（通り）です。

①と②は同時に起こるので、積の法則より4×8＝32（通り）です。

次のように場合分けして考えます。

① A→B、B→C、C→B、B→Aのどこでも10分か15分の交通手段（2通り）を利用する場合、必ず1時間（60分）以内になります。したがって、積の法則より2×2×2×2＝16（通り）です。

② A→BとB→Aでバスを利用する場合、B→CとC→Bではタクシーを利用するので1通りです。

③ A→BかB→Aのどちらかでバスを利用する場合を考えます。A→B がバスの場合、B→C、C→B、B→Aの合計時間が40分以内になるように樹形図を描くと、次の通りです。

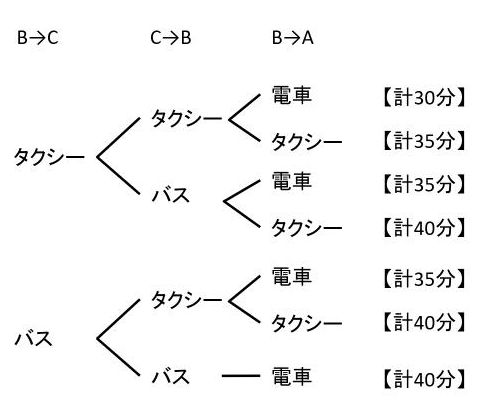
B→Aがバスの場合も同じように考えられるので、7×2＝14（通り）です。

④ B→CかC→Bのどちらかが徒歩の場合を考えます。（A→B、B→C、C→B、B→A）が（電車、徒歩、タクシー、電車）か（電車、タクシー、徒歩、電車）の2通りです。

①～④は同時に起こらないので、和の法則より16＋1＋14＋2＝33（通り）が答です。

① 順列と組合せの違いは何ですか。

（例）順列は並び順を考える場合の数で、組合せは並び順を考えない場合の数です。

② 和の法則を使う問題と積の法則を使う問題はどのように区別しますか。

（例）事柄AとBについて、AかBのどちらかが起こる場合の数を考えるときは和の法則を使います。一方、AとBのどちらも起こる場合の数を考えるときは積の法則を使います。

トップ画像＝Pixabay