問題演習コーナー
【問題】下の図の三角形ABCについて、AP:PC=3:1、BQ:QC=1:1、CR:RA=2:1です。三角形PQRの面積が35cm2のとき、三角形ABCの面積は何cm2ですか。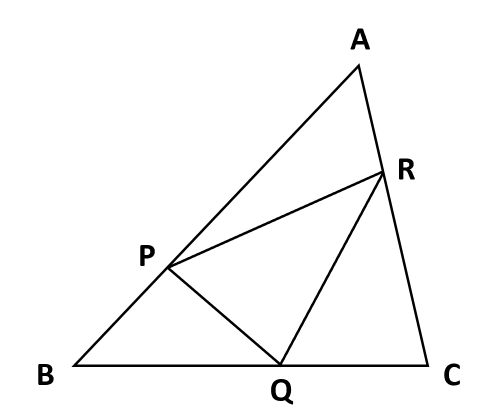
三角形ABCの面積を1とします。
- 三角形APRの面積=三角形ABCの面積×\(\frac{AP}{AB}\)×\(\frac{AR}{AC}\)=1×\(\frac{3}{4}\)×\(\frac{1}{3}\)=\(\frac{1}{4}\)
- 三角形BPQの面積=三角形ABCの面積×\(\frac{BP}{BA}\)×\(\frac{BQ}{BC}\)=1×\(\frac{1}{4}\)×\(\frac{1}{2}\)=\(\frac{1}{8}\)
- 三角形CQRの面積=三角形ABCの面積×\(\frac{CQ}{CB}\)×\(\frac{CR}{CA}\)=1×\(\frac{1}{2}\)×\(\frac{2}{3}\)=\(\frac{1}{3}\)
- 三角形PQRの面積=三角形ABCの面積-(三角形APRの面積+三角形BPQの面積+三角形CQRの面積)=1-(\(\frac{1}{4}\)+\(\frac{1}{8}\)+\(\frac{1}{3}\))=\(\frac{7}{24}\)
したがって、三角形ABCの面積=三角形PQRの面積÷\(\frac{7}{24}\)=35×\(\frac{24}{7}\)=120cm2が答です、
トップ画像=写真AC


コメント