【過不足算】線分図や面積図を描けば個数や人数を簡単に求められる！

問題演習コーナー

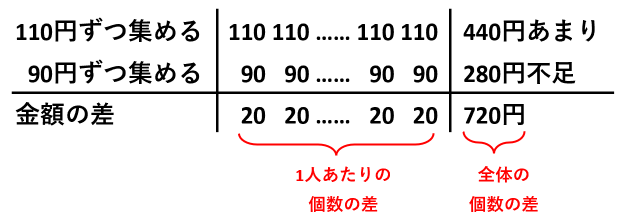
1人あたりの金額の差は110ー90＝20円です。一方、あまりが440円で不足が280円なので、全体の金額の差はあまりと不足の和で440＋280＝720円です。

「人数＝全体の金額の差÷1人あたりの金額の差」より、クラスの人数は720÷20＝36人です。したがって、花の値段は110×36ー440＝3520円です。

シイタケくん

110円ずつ集めると、花の値段よりも多くお金が集まるよ。だから、花の値段を求めるには、あまりの440円を集めたお金（110×36円）から引くんだ。

線分図を利用した解き方

2本の線を花の値段、クラス全員の人数を□人とします。

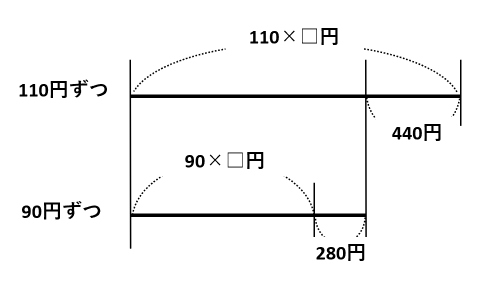
上の線には、110円ずつ□人から集めた金額（110×□円）とあまり（440円）を書き込みました。

同じように、下の線には90円ずつ□人から集めた金額（90×□円）と不足（280円）を書き込みました。

エノキさん

あまりがあるときは、お花の値段より多く集めたときなので、線を右側に伸ばすのよ。逆に、不足があるときは、お花の値段より少なく集めたときなので、線の右端を切り取るのよ。

線分図を見ながら、110×□ー90×□＝（110ー90）×□＝20×□円と440＋180＝720円を書き足しましょう。

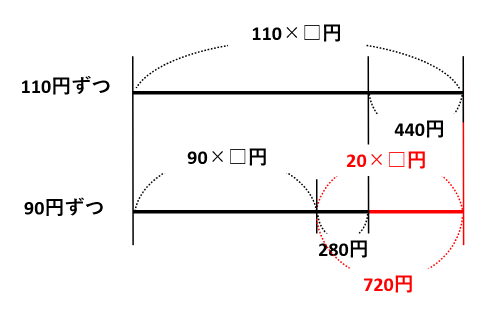
20×□＝720なので、□＝720÷20＝36人が人数です。したがって、花の値段は110×36ー440＝3520円です。

面積図を利用した解き方

縦に1人あたりの金額、横に人数を書いた面積図を描きます。

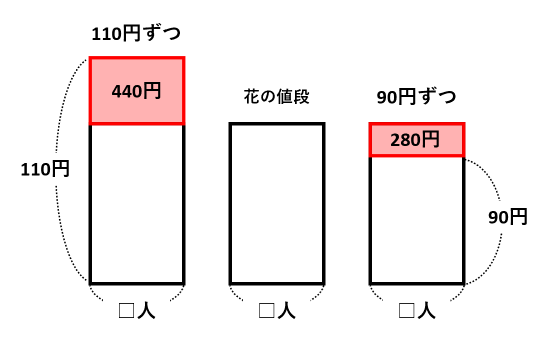
これら3つの図を1つに合わせると、次の図になります。

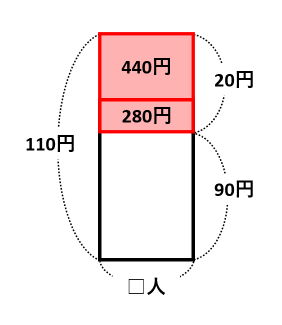
440＋180＝720円の長方形を見て、20×□＝720から□＝720÷20＝36人が人数です。したがって、花の値段は110×36ー440＝3520円です。

トップ画像＝写真AC