中学受験や高校受験の算数・数学で最も難しいのが図形です。平面図形と空間図形の2分野があって、難関校を中心に、毎年眩暈を覚えるような問題が出題されます。
図形問題が難しいのはなぜでしょうか？
計算量が多い、発想が難しいなどの理由があります。その中でも図形問題ならではの理由は、補助線を引かなければならないことです。
本記事では、補助線の引き方のコツを紹介します。
どうしてそこに補助線を引くの？
補助線とは、問題を解くために自分で図形に描き込んだ線のことです。この補助線の引き方が分からなくて、図形問題でフリーズする生徒がたくさんいます。
算数（数学）講師の中には、「図形問題はパターンだから、たくさん問題を解いて解法を暗記しなさい」という人がいます。
たしかに、補助線の引き方も含めて、図形問題はパターン暗記で何とかなる問題も少なくありません。しかし、パターン暗記の勉強法では、典型問題は解けても未知の問題には対応できません。
そこで大切になるのは、「どうしてそこに補助線を引くの？」ということです。
図形に補助線を引くための2つの視点
図形に補助線を引くための2つの視点を紹介します。
1. 必要な情報を求めるため
次の【例題1】を考えてみましょう。
【例題1】下の三角形は、角Aが30°、ABとACの長さが10cmの二等辺三角形です。面積は何cm2ですか。
この問題では「三角形の面積」を求めなければなりません。そこで、三角形の面積公式である「底辺×高さ÷2」を思い浮かべます。
AB=10cmと分かっているのでABを底辺とします。高さは底辺に垂直な線分です。しかし、図の中には、ABに垂直な線分がありません。そのため、CからABに垂線を下ろして、垂線の足をHとします（下図の赤線）。
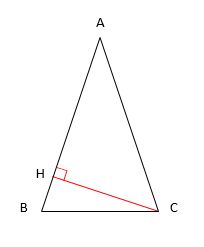
ここで、三角形ACHは、正三角形を半分にした特殊な三角形なので、CHはACの\(\frac{1}{2}\)倍で5cmになります。
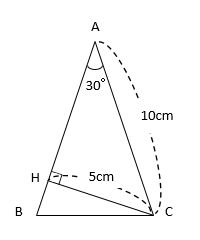したがって、三角形ABCの面積は10×5÷2＝25（cm2）です。
この問題では、三角形ABCの高さを求めるために補助線を引きました。つまり、必要な情報を求めるために補助線を引きました。
このような視点で補助線を引く場合、まずは「自分が何をしたいのか？」を明確にする必要があります。
【例題1】では、「三角形の面積を求めるために面積公式を利用する」という方針があって初めて「高さが必要だ」と気づきます。「角Aが30°だから、とりあえず他の角が60°（もしくは90°）になる三角形を作っておこう」といういい加減な理由で補助線を引くわけではありません。
2. 与えられた情報を利用するため
次に、【例題2】を考えてみましょう。
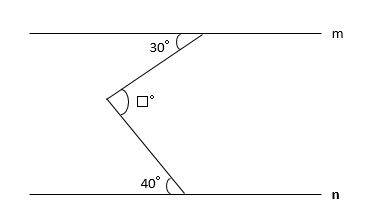
【例題2】下の図で、直線mと直線nは平行です。このとき、□の大きさを求めなさい。
有名な問題なので、ほとんどの生徒は補助線の引き方を知っていると思います。
直線mと直線nに平行で□を二分する直線を引きます（下図の赤線）。
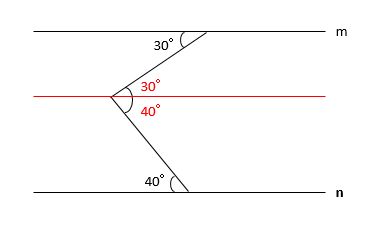
平行線の錯角は等しいので、図のように□＝30＋40＝70（°）と分かります。
【例題2】では、補助線を引いて平行線の錯角を作って、□を30°と40°の和に置き換えました。つまり、与えられた情報を利用するために補助線を引いたのです。
このような視点で補助線を引く場合、与えられた情報を活かすための公式や定理などを知っている必要があります。
平行線を引くのは、錯角や同位角を作るためか等積変形を行うためです。こうした目的がないのに平行線を引いても、邪魔な線が増えるだけです。
補助線の引き方が合否を決する
算数や数学の問題は、1問の配点が高く、その1問を解けたかどうかが合否を左右します。そして、図形問題では、補助線をどこに引くかで問題が解けたり解けなかったりします。つまり、補助線の引き方が合否を決するのです。
パターン暗記に頼っている生徒の多くは、「とりあえず」で適当に補助線を引いて、その後に「あれ？何をすればいいの？」と混乱します。
そうならないために、「必要な情報を求めるために補助線を引く」「与えられた情報を利用するために補助線を引く」という2つの視点を大切にしながら図形問題を解くようにしましょう。
トップ画像＝Pixabay
コメント