12は2や3で割り切れます。このように、12を割り切れる2や3を「12の約数」といいます。
本記事では、約数の基本、公約数の求め方、「互いに素」の意味についてわかりやすく解説します。
約数・公約数・最大公約数とは何か?
約数とは、ある整数を割り切れる数です。約数は必ずかけ算の形で求めましょう。たとえば、12の約数と20の約数はそれぞれ次のように求めます。
- 12の約数:1×12、2×6、3×4 → 1、2、3、4、6、12
- 20の約数:1×20、2×10、4×5 → 1、2、4、5、10、20
かけ算のかける数とかけられる数がどちらも約数になります。
どの整数も「1×自分自身」と表せるので、1はすべての整数の約数です。一方で、0.5や\(\frac{2}{3}\)など、小数や分数は約数ではありません。
12の約数と20の約数では、下線を引いた1、2、4が共通します。このように、2つ以上の整数に共通する約数が公約数です。
12と20の公約数の中で最も大きいのが4です。このように、最も大きい公約数が最大公約数です。
1、2、4を見ると、1も2も4の約数です。12と20の公約数に限らず、「公約数は最大公約数の約数」が成り立ちます。
最大公約数の求め方を理解する
「公約数は最大公約数の約数」なので、公約数を求めたければ、まずは最大公約数を求めます。その求め方を紹介します
最大公約数を素因数分解で求める
12の約数と20の約数を書き並べずに4を求めてみましょう。
まずは、12と20を素因数分解します。素因数分解とは、ある整数を素数の積(かけ算)で表すことです。
12と20をそれぞれ素因数分解すると、12=2×2×3、20=2×2×5です。2×2=4が両方に共通していて、この4が12と20の最大公約数です。
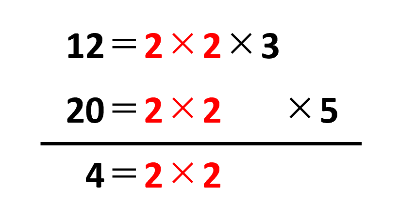
約数の個数を求めるときも素因数分解を利用します。詳しくは以下の記事で確認しましょう。

すだれ算(連除法・はしご算)とは何か?
素因数分解を利用した最大公約数の求め方をもっと簡単にしたのがすだれ算(連除法・はしご算)です。
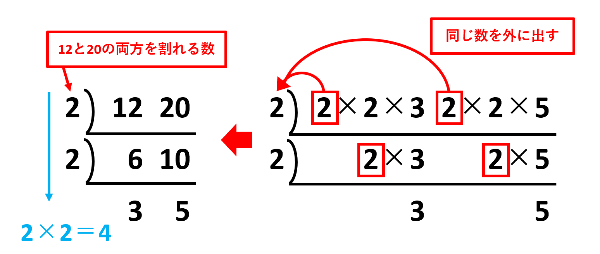
下の図のように、12と20を並べて、割り算の筆算をひっくり返したような計算をします。12と20の両方を割れる2を左に書いて、横棒の下に商の6と10を書きます。6と10の両方を割れる2を左に書いて、横棒の下に商の3と5を書きます。3と5の両方を割れる数が1しかないのでここで終了です。最後に、左に書いた2と2をかけて2×2=4が12と20の最大公約数です。
最大公約数の求め方は最小公倍数の求め方とほとんど同じ手順ですが、最後にかける数が違います。その違いを以下の記事で確認しておきましょう。

3つの整数の最大公約数をすだれ算で求める
3つの整数の最大公約数もすだれ算で求められます。
12と18と30の最大公約数を求めるすだれ算は下の図のようになります。左に書くのは、3つすべてを割れる数です。2と3と5の3つすべてを割れる数が1しかないのでここで終了です。最後に、左に書いた2と3をかけて2×3=6が最大公約数です。
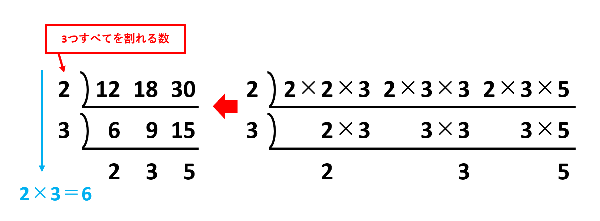
6と8と9のように、はじめから3つすべてを割れる数がなければ、最大公約数は1です。
ユークリッドの互除法とは何か?
2つの整数の最大公約数はユークリッドの互除法でも求められます。
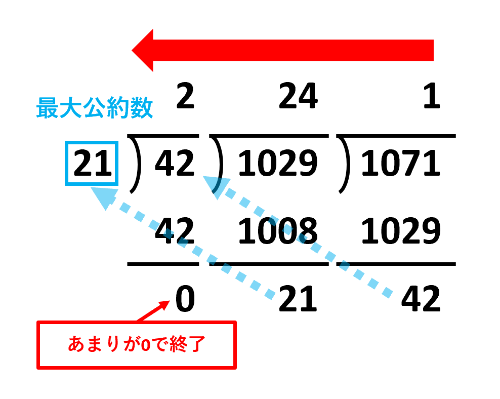
例として、1029と1071の最大公約数を求めましょう。まずは、大きい方を小さい方で割ります。続いて、前の式の割る数をあまりで割ります。これをくり返していって、あまりが0になったときの割る数の21が最大公約数です。
1071÷1029=1あまり42
1029÷42=24あまり21
42÷21=2(終了)
したがって、1029と1071の最大公約数は21
この計算を「割られる数=割る数×商+あまり」の式で表すと次の通りです。
1071=1029×1+42
1029=42×24+21
42=21×2(終了)
したがって、1029と1071の最大公約数は21
ユークリッドの互除法を下のような筆算で計算することもできます。

1029と1071のように、桁数の大きい整数の最大公約数を求めるときに、ユークリッドの互除法が便利だわ!
最大公約数が1である2つの整数は互いに素
2つの整数について、両方を割れる整数が1以外に存在しない場合、これらの整数の最大公約数は1です。このように、最大公約数が1である2つの整数を「互いに素」といいます。
2と3、7と9、8と15などは互いに素ですが、2と4(最大公約数は2)、6と9(最大公約数は3)、8と12(最大公約数は4)などは互いに素ではありません。
「互いに素」は「互いに素数」という意味ではないので注意しましょう。

14と15はどちらも素数ではない。でも、14と15の最大公約数は1だから、14と15は互いに素なんだ。「互いに素」を「互いに素数」と勘違いしないでね!
公約数に慣れると計算が楽になる
分数の計算では最後に約分します。約分とは、分子と分母を公約数で割ることです。\(\frac{14}{21}\)=\(\frac{2}{3}\)は、14と21の(最大)公約数である7で約分しました。
また、比を簡単にするときも、それぞれの数の公約数で割ります。64:40:32=32:20:16=16:10:8=8:5:4は、64と40と32の公約数で割っていきました。また、64と40と32の最大公約数の8で割れば、あっという間に8:5:4を求められます。
このように、公約数はさまざまな計算で使うので、公約数に慣れると計算が楽になります。
次の質問に答えましょう。(解答例は最後のページにあります)
① 約数とはどのような数ですか。
② 公約数とはどのような数ですか。
③ 公約数と最大公約数の関係を説明しましょう。
④ 「互いに素」を説明しましょう。


コメント