高校の数学Bでは「数列」を扱います。
数列分野は、最初のうちは簡単です。等差数列や等比数列までは中学数学の延長みたいな内容です。中学受験を経験した生徒なら、「等差数列なら知ってます!」と懐かしく思うかもしれません。
しかし、和の記号Σ(シグマ)が登場するあたりから雲行きが怪しくなってきます。この「Σ」なる記号は、実は赤点量産装置なんですね(笑)。
「Σの公式を覚えてるから大丈夫!」と高をくくっていると、公式を適用できない問題が登場して……定期テストの答案が真っ赤に!!
そんな悲劇を味わいたくない生徒は、Σの定義をしっかり確認して、公式丸暗記から脱却しましょう。
和の記号Σの定義
\(\displaystyle \sum_{k=1}^{10} k \)は「kが 1, 2, 3, …,10 と変わるときのkの値をすべて加えた和」という意味です。分かりにくいので図にすると次の通りです。
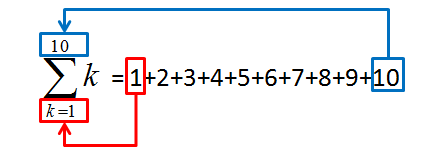
つまり、Σを使ったこの表現は、「1+2+3+4+5+6+7+8+9+10」と全く同じ意味なのです!
たとえば虚部を表すiや対数logは特別な数を表現します。一方、Σは、iやlogとは違って、長くなりがちな和の式を簡単に表記するための記号なのです。
ということは、「Σが分からない!」と思ったら、Σを使わない足し算の式に書き換えてみるといいわけですよ。
Σの公式を適用できない?
Σの定義を確認したところで、Σの公式にも軽く触れてみます。次の公式は有名ですね。
この公式を使ってサクサク問題を解こうと思っていると、突然悲劇が訪れます!
次の問題を考えましょう。
「公式が使えるじゃん!」と冒頭の公式の右側を解答欄に書いたら×ですよ。この問題は、kが100から始まっているので公式にそのまま当てはめられません。
こういうときは、Σの定義に戻って、足し算の式に書き換えてみます。
これは次のように変形できます。
1からnまでの総和から、1から99までの総和を引いています。
「1+2+3+・・・+98+99+100+101+102+…+(n-1)」と「1+2+3+・・・+98+99」をそれぞれΣで書き直すと次の通りです。
ここまで変形すれば、冒頭の公式に当てはめて計算できます。
k=0から始まる場合は?
間違いの多い変形をもう少し考えます。次の計算をしてみましょう。
よくある誤答例は次の通りです。
どこが間違っているのでしょうか?
誤答例では、次の公式を適用したと考えられます。
\(\displaystyle \sum_{k=1}^{n} k^2 = \frac{1}{6}n(n+1)(2n+1) \)
\(\displaystyle \sum_{k=1}^{n} 1 = n \)
しかし、【問題2】の式はkが1から始まっていない以上、公式にそのまま当てはめられません。誤答例は、【問題1】と同じ過ちを犯しています。
kの2乗の和
\(\displaystyle \sum_{k=1}^{n} k^2 = \frac{1}{6}n(n+1)(2n+1) \)の左辺は、「kの2乗で表される式にk=1,2,3,…,nを代入していき、それらを全て足し合わせる」という意味です。これをΣを使わずに書けば、次のようになります。
同じように、k=0で始まる場合もΣを使わずに書いてみます。0の2乗は0なので無視すると、k=0で始まる式は、k=1で始まる式と同じであることがわかります。
したがって、誤答例の\(\frac{1}{6}\)の項は正しかったわけです。とはいえ、これは、たまたま正しかっただけです。
1の和
\(\displaystyle \sum_{k=1}^{n} 1 = n \)の左辺は、「1番目からn番目まで1で表される数列をすべて足し合わせる」という意味です。つまり、1が全部でn個あるので、その総和がnなのです。
この公式のk=1がk=0に変わったらどうでしょうか?
k=1で始まる公式に0番目の1が加わるので、上のように書き換えました。この結果から、k=0で始まる式は、k=1で始まる式と同じにならないことがわかります。
以上より、誤答例を正しく直すと次の通りです。
和の記号Σに振り回されるな!
数列分野では、和の記号Σという記号に振り回されず、きちんと意味を考えることが大切です。そうしないと、恐怖の赤点地獄に堕ちてしまいますよ!(笑)
トップ画像=Pixabay




コメント
分かりやすい解説ありがとうございます!!
ずっとわからなかった疑問が解消しました
お役に立てて良かったです。
僕自身も高校時代、数列で赤点を取りかけました。
当時、きちんとシグマの意味を理解していたらなぁ、と思っています(笑)
ラブラドールさんがシグマを使いこなして数列が得意になることを願っています!