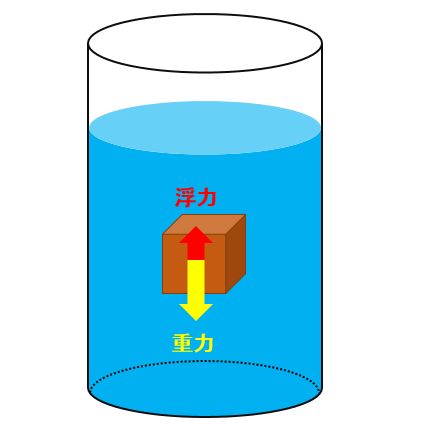
中学理科の第1分野で学ぶ「力」の分野では浮力を学びます。
浮力とは、水中にある物体にはたらく上向きの力です。物体を水の中に沈めようとしても浮き上がってきますよね?この「浮く」という現象を引き起こすのが浮力なんですね。
多くの中学1年生が浮力を学びます。教科書の範囲内であれば、「物体の水に沈んでいる部分の体積が大きいほど、はたらく浮力は大きい」と教わるだけです。
しかし、中学理科の先生たちの中には、浮力の計算問題を出題する先生がいます。そんな先生の作成する定期試験対策として、浮力の計算についてきちんと解説します。
アルキメデスの原理
浮力とセットで登場する考え方に「アルキメデスの原理」があります。これは、その名前の通り、古代ギリシアの数学者・物理学者アルキメデスが発見した原理です。意味は、「流体中で静止している物体は、それが押しのけた流体に働く重力と等しい浮力を受ける」です。
アルキメデスの原理で登場する「流体」とは、水やアルコールなどの液体や空気などの気体です。中学理科で浮力を扱う場合、普通は水を考えます。
「それ(物体)が押しのけた流体に働く重力」は、物体が無ければそこにあるはずの水の重さのことです。
たとえば、1cm3の立方体の木片が水に沈んでいるとき、その木片にはたらく浮力は1g=0.01Nです(水の密度を1g/cm3、重力の単位換算を100g=1Nとします)
この浮力の値は、木片が水深何mの位置にあっても変わりません。浮力は水深の影響を受けず、物体の体積にのみ比例します。
浮力が生じる理由
浮力が物体の体積に比例するのはなぜでしょうか?
1cm3の立方体の木片が、下図のように水に沈んでいる場合を考えましょう。
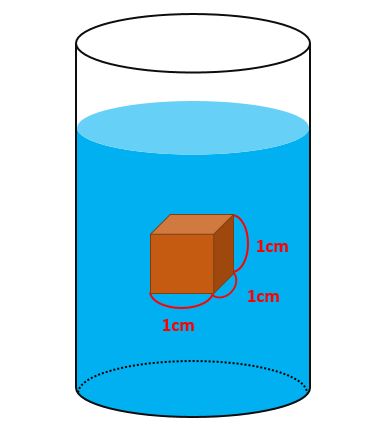
このとき、木片に働く力を図示すると次の通りです。
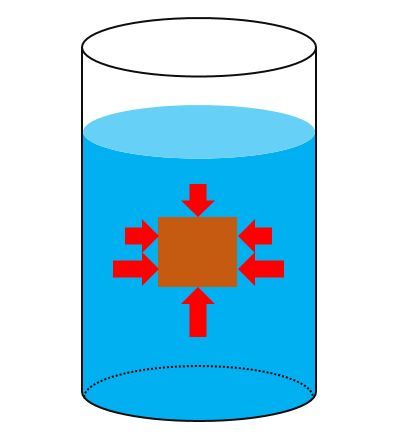
水が面を押す力は水深に比例すること、この力はあらゆる方向からはたらくことの2点を踏まえて矢印の向きと長さを調整しました(矢印が長いほど力も大きい)。
水平方向の力は、お互いに反対向きで大きさも等しいため、打ち消し合います(木片に影響を与えない)。
一方、垂直方向の力は、木片の上面にはたらく力(下向きの力)よりも下面の力(上向きの力)の方が大きくなっています。したがって、上向きの力は、下向きの力の分だけ打ち消されますが、完全には打ち消されません。打ち消されずに残った力が浮力となります。
浮力=上向きの力-下向きの力
実際の数値を使って浮力を計算してみます。まずは、下向きの力を求めます。
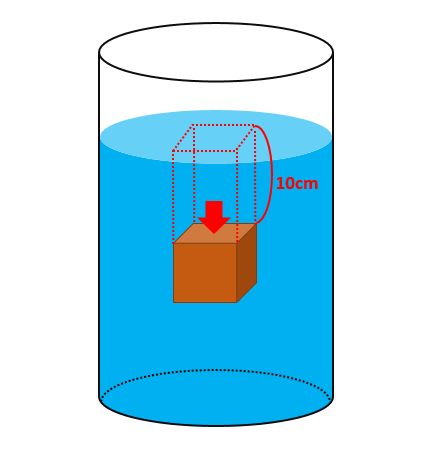
下向きの力は、木片の上面に乗っている水の重さ(重力)です。この重さは、「水の体積×水の密度」で計算します。
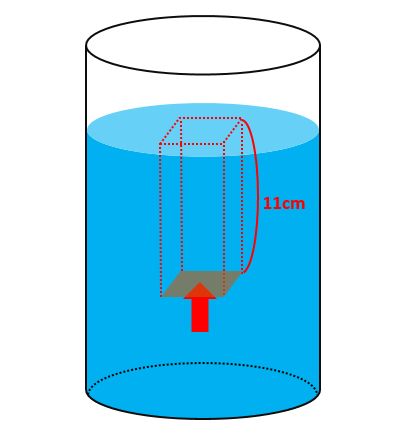
(2) - (1)
= 11cm×1cm2×1g/cm3-10cm×1cm2×1g/cm3
= (11cm-10cm)×1cm2×1g/cm3
= 1cm×1cm2×1g/cm3
= 1cm3(木片の体積)×1g/cm3(水の密度)
以上の計算から、浮力は水深の影響を受けず、物体の体積にのみ比例することが明らかになりました!!
というわけで、水の密度を1g/cm3、重力の単位換算を100g=1Nとするとき、1cm3の物体にはたらく浮力は1g=0.01Nです。cm3単位で体積を考えるとき、「浮力(N)=体積(cm3)×0.01」という公式が成り立つのです。
物体が沈む=物体の重さ>浮力
浮力は物体の体積のみに比例します。しかし、同じ大きさの物体を水に沈めたとき、重い(密度が大きい)方の物体の方が軽い(密度が小さい)物体よりも深く沈みます。どちらの物体にも同じ大きさの浮力が働いているはずなのに、どうして違いが生じるのでしょうか?
物体にはたらく力には何があるでしょうか?
冒頭で検討した通り、物体には浮力がはたらきます。それ以外にも、物体には重力がはたらくことを忘れてはいけません。物体には重さがありますよね。
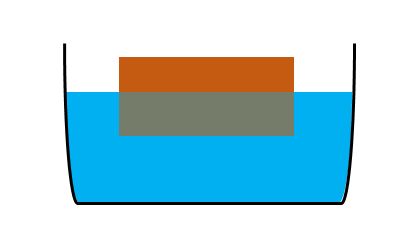
たとえば、次の図のように、物体の重さ(物体にはたらく重力)が浮力より大きければ、浮力に打ち消されない重力(下向きの力)によって物体は沈みます。
逆に、物体にはたらく重力が浮力より小さければ、物体は浮き上がります。また、物体にはたらく重力と浮力が等しければ、物体は静止します。
重力(物体の重さ)の影響で、同じ体積の物体でも浮き沈みに違いが生じるのです。
浮力の計算問題にチャレンジ
浮力と物体の重さとの関係を理解できたところで、定期試験などに頻出の計算問題にチャレンジしましょう。
下の図のように、体積100cm3の木片を水の中に入れたら浮かびました。このとき、木片の水中の部分の体積は80cm3でした。次の問いに答えなさい。
(1)木片にはたらく浮力の大きさは何Nですか。
(2)この木片の質量は何gですか。
(3)この木片の密度は何g/cm3ですか。
(1)は、水の中に入っている部分の体積だけを考えて浮力を求めます。問題文中に「水中の部分の体積は80cm3」とあるので、前ページで求めた公式「浮力(N)=体積(cm3)×0.01」に体積を代入して、0.8Nが答です。
(2)は、浮力と木片の重さがつり合っていると考えます。つまり、“浮力=木片の重さ”なので、0.8N=80gより80gが質量です(特別な指定が無い限り、「重さ」と「質量」は同じ数値で大丈夫です)。
(3)は、密度の公式から考えます。「密度(g/cm3)=質量(g)÷体積(cm3)」です。(2)より木片の質量は80gで、問題文より木片の体積は100cm3です。したがって、密度は、80g÷100cm3=0.8g/cm3です。
浮力の計算問題は簡単
浮力の計算問題は中学受験理科でも頻出です。小学生でも理解できるレベルなんですね。

「浮力の計算が苦手」という中学生は、その思い込みを捨てて、じっくり問題と向き合ってみてください。理屈が分かればとても簡単に計算できますよ!!
トップ画像=Pixabay




コメント