【量の単位のしくみ】SI接頭辞がわかれば単位換算も簡単にできる！

多くの中学受験生は、3kmを300000cmに変換するような問題を苦手とします。「1kmは1000mで、1mは100cmで……」というバラバラの知識のせいで混乱するからです。

このような混乱を防ぐには、小学6年の算数で最後に学習する「量の単位のしくみ」を理解するのがおすすめです。

本記事では、「量の単位のしくみ」をふまえて単位換算のコツを解説します。

オカルト進学塾

志望校合格とオカルトエリートを目指す受験勉強サイト

occult-shingakujuku.com

「量の単位のしくみ」で学ぶSI接頭辞

「mL」は一つの単位ではなく、「m（ミリ）」と「L（リットル）」に分かれます。このことがわかると、「m（ミリ）」は「m（メートル）」や「g（グラム）」とくっついて「mm（ミリメートル）」や「mg（ミリグラム）」になっていることにも気づくはずです。

体積や長さなどの単位とくっつく「m（ミリ）」や「k（キロ）」などを「SI接頭辞」といいます。このSI接頭辞のうち、中学受験レベルで使うものは次の表の通りです。

シイタケくん

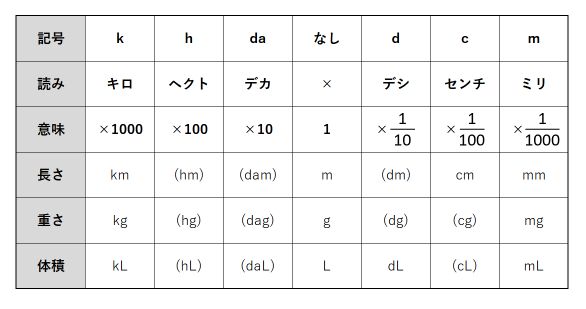
日本ではdaやhをあまり見ないけど、しっかり覚えよう。特にdaとdをまちがわないでね！

たとえば、「k」を「×1000」に書きかえれば、「3km＝3×1000m＝3000m」と計算できます。一方、次の例題1はどうでしょうか？

例題1は「3km＝3000m」よりも難しいと思います。しかし、小数点の移動を使えば、このような単位換算も簡単に解けます。

単位換算を小数点の移動と考える

たとえば、3.14×10＝31.4、3.14×100＝314…のように、ある数に10、100、1000…をかけると、小数点が右に1つ、2つ、3つ…と移動します。一方、3.14×\(\frac{1}{10}\)＝0.314、3.14×\(\frac{1}{100}\)＝0.0314、3.14×\(\frac{1}{1000}\)＝0.00314…のように、ある数に\(\frac{1}{10}\)、\(\frac{1}{100}\)、\(\frac{1}{1000}\)…をかけると、小数点が左に1つ、2つ、3つ…と移動します。

単位換算でも同じように小数点の移動を使えます。

まず、SI接頭辞を書き並べます。左から「k（キロ）、h（ヘクト）、da（デカ）、×（なし）、d（デシ）、c（センチ）、m（ミリ）」とし、真ん中には「×」を必ず入れてください。

次に、もとの単位から換算後の単位まで、左右どちらの方向にいくつ移動したかを考えます。最後に、単位の移動と同じ方向に同じ個数分だけ小数点を移動します。

たとえば、3kmの単位をmに変えたい場合、kから×まで右に3つ移動していることがわかります。

同じように3の小数点を右に3つ移動して、3km＝3000kmです。

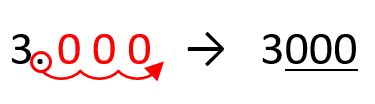
同じ手順で35000cmの単位をkmに変えてみましょう。cからkまで左に5つ移動します。

同じように35000の小数点を左に5つ移動して、35000cm=0.35kmが例題1の答です。

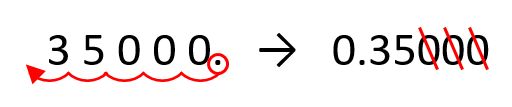
実際のテストでは、テスト開始直後、問題用紙の空白に「k、h、da、×、d、c、m」を書き、それを見ながら単位換算するといいでしょう。

エノキさん

真ん中に×を入れるのを忘れないでね！

面積や体積の単位換算には要注意

例題2では、多くの受験生は「小数点を右に3つ移動するだけだから3000m²です」と答えます。しかし、これはまちがいです。

なぜなら、面積の単位換算は次のように考えなければならないからです。

面積の単位は、「m（メートル）」の右上に小さな「2（平方）」が付いています。これは、同じものを2回かける目印です。したがって、小数点の移動も2回行う必要があります。

3km²の単位をm²に変える場合、小数点を右に3つ移動×2回です。したがって、3の後ろに0が6つくっついて、3km²＝3000000m²が正解です。

同じように考えて、3km³の単位をm³に変える場合、小数点を右に3つ移動×3回で3km³＝3000000000m³となります。

小数点の移動を使えない単位換算

例題3ではこのままでは小数点の移動を使えません。そこで必要となるのが次の4つのルールです。

シイタケくん

上の2つは、数字が同じで単位だけが変わっているんだ。

4つのルールをふまえて、0.5dLの単位をcm³に変えてみます。

まず、4つのルールにcm³はありますが、dLはありません。ルールを使うため、小数点の移動でdLをmLに変えます。小数点を右に２つ移動して0.5dL＝50mLです。

次に、ルールを使って、mLをcm³にそのまま書きかえます。したがって、50mL＝50cm³なので 0.5dL＝50cm³が答です。

アールやトンの単位換算にチャレンジ

(1)の解答（面積の単位換算）

ルール通り、m²をaに書きかえます。その後、aを「h」の付いているhaに直すので、小数点を左に2つ移動します。

(2)の解答（重さの単位換算）

gをkgに書きかえるため、小数点を左に3つ移動します。その上で、ルール通り、kgをtに書きかえます。

小数点の移動と4つのルールを合わせて使うと、aやtの単位換算も簡単に解けるようになります。

エノキさん

SI接頭辞にはk～m以外に何があるんですか？

エリンギ先生

大きな数を表すSI接頭辞で、日常的に使うものとしては、M（メガ）・G（ギガ）・T（テラ）があるよ。Mは「×百万」、Gは「×十億」、Tは「×一兆」を表すんだ。

シイタケくん

パソコンやスマホの容量を表す「メガバイト」や「ギガバイト」の「メガ」や「ギガ」ですね！

エリンギ先生

その通り！逆に小さな数を表すSI接頭辞は、μ（マイクロ）やn（ナノ）を聞いたことがあるんじゃないかな？μは「×百万分の一」、nは「×十億分の一」だよ。

エノキさん

「マイクロチップ」や「ナノマシン」という言葉は、SI接頭辞から来てるんですね！

SI接頭辞は中学以降の勉強にもつながる

公立小学校で「量の単位のしくみ」を習うのは6年の最後です。しかし、中学受験生は、小数計算ができるようになったら、すぐにSI接頭辞を覚えて使うようにした方がいいでしょう。

SI接頭辞は算数のすべての分野で大切です。たとえば、面積・体積や速さの問題では、単位換算ができないと解けない問題も少なくありません。

また、中学受験の理科でも、単位換算をしなければならない問題があります。さらに、中学進学後、単位換算がよくわかっていないと、密度や力などの計算問題ができなくなってしまいます。

小学生のうちにSI接頭辞に慣れておくことが、中学以降の勉強にもつながります。