都立高校入試数学の大問4は平面図形に関する問題です。
平成29年度の大問4は、長方形に内接する半円が題材でした。例年通り、比較的平易な[問1]と完全記述式の[問2]の①、そしてやや難の[問2]の②の3問です。
本記事では、これらの3問をわかりやすく解説します。
扇形の弧の長さを求める問題
[問1]は、扇形の弧の長さを求める典型的な問題です。まずは、弧の長さの公式を思い出しましょう。
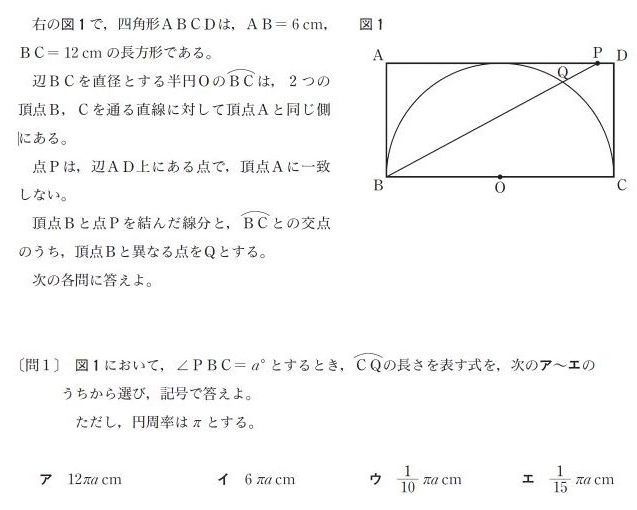
今回の問題では、直径の長さはBC=12cmです。
一方、中心角は∠PBC=a°ではないので要注意です。下図のように、OとQを結ぶ補助線を引いたときの∠QOCが中心角です。
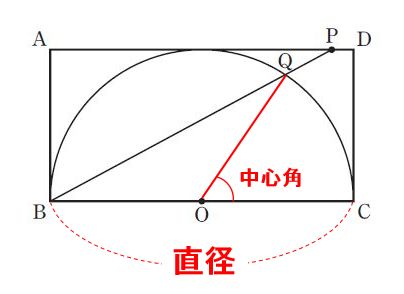
∠PBC(∠QBC)と∠QOCは、弧QCに対する円周角と中心角の関係です。したがって、∠QOC=2∠PBC=2a°です。
直径の長さと中心角の大きさを公式に当てはめると、正解はエです。
公式発表によると、[問1]の正答率は42.7%と低めです。弧の長さを求める公式を覚えていない受験生や、直径や中心角を間違った受験生が多かったのでしょう。
三角形の相似を証明する問題
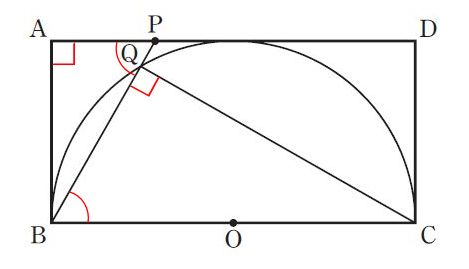
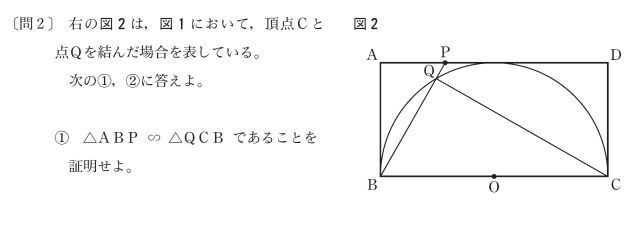
三角形の相似を証明する問題では、「2組の角がそれぞれ等しい」という相似条件を用いることがほとんどです。[問2]の①も、この相似条件を用いるために、2組の等しい角を探します。
ここで注目したいのが、四角形ABCDの性質です。四角形ABCDは長方形なので、以下の条件が隠れています。
△QCBは円に内接する三角形で、BCが直径です。したがって、∠BQC=90°です。アと合わせて∠BQC=∠PAB=90°なので、1組の等しい角が見つかりました。
また、イから、平行線の錯角は等しいので∠APB=∠QBCと分かり、もう1組の等しい角が見つかりました。
以上より、次のような解答例になります。
△ABPと△QCBにおいて、
四角形ABCDは長方形だから、
∠PAB=90°
半円の弧に対する円周角は直角だから、
∠BQC=90°
よって、
∠PAB=∠BQC …… (1)
長方形の対辺は平行だから、AD∥BC
平行線の錯角は等しいから、
∠APB=∠QBC …… (2)
(1)、(2)より、2 組の角がそれぞれ等しいから、
△ABP∽△QCB
線分の長さを求める問題
[問2]の②のような問題では、「答を求めるためには、どこの線分の長さが必要か?」と考えます。
[問2]の②で求めるべき答えはPQの長さです。PQ=PB-QBなので、PBとQBの長さが必要だと分かります。
また、[問2]の②では、ほとんどの場合、①で証明した事柄を利用します。本問でも、PBとQBがそれぞれ△ABPと△QCBの一辺なので、間違いなく△ABP∽△QCBを利用するはずです。そこで、下図のように、△ABPと△QCBを、向きをそろえて抜き書きします。このとき、長さの分かる辺には数値を書き込みましょう。
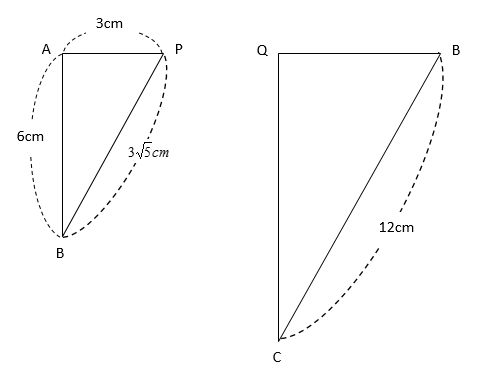
AD=BC=12cmで、AP:PD=1:3なので、APはADの\(\frac{1}{4}\)倍で3cmです。また、△ABPに三平方の定理を用いて、BPの長さも求めました。
\(BP^2=AB^2+AP^2\)
\(BP=\sqrt{6^2+3^2}=3\sqrt{5}\)(cm)
△ABP∽△QCBなので、相似比を用いてQBの長さを求めます。その後、PQ=PB-QBからPQの長さを求めます。
AP:QB=BP:CB
3:AP=3\(\sqrt{5}\):12
QB=\(\frac{3×12}{3\sqrt{5}}=\frac{12\sqrt{5}}{5}\)
PQ=PB-QB=3\(\sqrt{5}-\frac{12\sqrt{5}}{5}\)=\(\frac{15\sqrt{5}}{5}-\frac{12\sqrt{5}}{5}\)=\(\frac{3\sqrt{5}}{5}\)(cm)
図形分野で差を付ける
平成29年度の大問4は、これといった捻りもなく、素直に解ける平易な問題でした。
それにもかかわらず、全体の正答率は決して高くありませんでした。相似や三平方の定理を学ぶのが中学3年の後半なので、多くの都立高校受験生がこれらの単元を定着させられずに入試に臨んでいるかもしれません。
逆にいえば、相似や三平方の定理を早めに学習し、図形の問題に慣れておけば、他の受験生に差を付けられるはずです。
都立高校合格を目指す受験生は、夏休みを利用して中3の図形分野を先取りした後、過去10年の都立高校入試問題を徹底分析して分野別にまとめた問題集「高校入試 虎の巻![]() 」を使って過去問をたくさんこなしましょう。
」を使って過去問をたくさんこなしましょう。
トップ画像=Pixabay





コメント