次の問題を考えてみましょう。
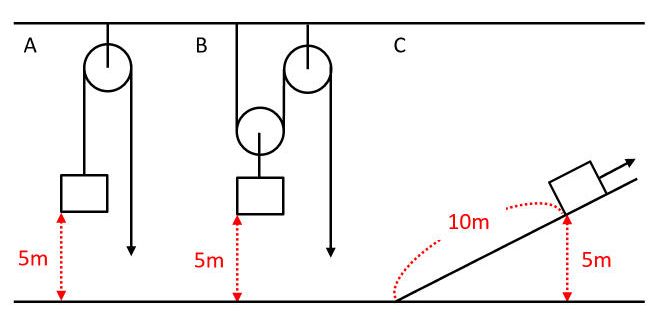
質量10kgの物体を5mの高さまで引き上げるのに、Aでは定滑車を、Bでは動滑車を、Cでは斜面を使った。A、B、Cで、同じ速さ(0.5m/s)でロープを引いたときのそれぞれの仕事率を求めなさい。ただし、ロープや滑車の質量、摩擦は考えないものとし、100gの物体にはたらく重力の大きさを1Nとする。
この問題を見て「わからない!」と頭を抱える生徒続出!
というのも、教科書のどこを見ても、仕事率と速さの関係について書かれていないからです。生徒たちは「教科書の書かれていないことを問題にしないで!」と文句を言います。
では、この問題は解けないのでしょうか?
もちろんそんなはずはありません。今回は、初見の問題の解き方について解説します。
単位に着目して公式を導こう
確かに、仕事率と速さの関係について教科書には書かれていません。しかし、今回の問題は、教科書で習った知識を使って解けます。
では、どうやって問題を解けばいいのでしょうか?
理科では、初見の問題でも、単位に着目することで解けることがあります。単位というのは、「kg」「m」など、数字の後ろにくっついている記号のことです。
実際に単位に着目して考えましょう。
まず、仕事率の公式は知っておく必要があります。
「s」は「秒」を表します。理科では、多くの場合、時間の単位を秒(s)にします。
次に、仕事の公式も確認しましょう。
仕事と仕事率の公式は、どんな教科書にも記載があるはずです。これらを覚えておかないと何もできません。
さて、①と②を単位だけで書き直してみます。
W = J/s ……①
J = N×m ……②
「/」は「÷」と同じです。「2÷3」は「2/3」と表されます。この2/3は\(\frac{2}{3}\)のことです。
②を①に代入してみましょう。
m/sをどこかで見たことありませんか?
問題文に書いてあった速さの単位ですよね?
このことに気づけば、仕事率と速さについて次の公式が成り立つとわかります。
“仕事率=力×速さ”を使ってみよう
③の公式を使えば、A、B、Cのそれぞれの仕事率を求められます。10kg=10000g=100Nです。
Aの定滑車を使った場合、物体にかかる力とロープを引く力は等しいので、ロープを引く力は100Nです。したがって、仕事率は100×0.5=50(W)です。
Bの定滑車を使った場合、2本のロープが動滑車についているので、ロープを引く力は物体にかかる力の半分の50Nになります。
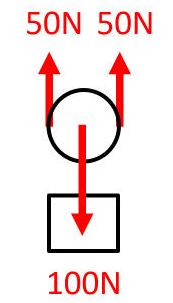
したがって、仕事率は50×0.5=25(W)です。
Cの斜面を使った場合、上で紹介した仕事の公式(②)から、ロープを引く力の大きさを求めます。
同じ質量の物体を同じ高さに持ち上げるのに必要な仕事の大きさはどんな方法を使っても同じ(仕事の原理)なので、(斜面でロープを引く力)×100(m)=100(N)×50(m)より、斜面でロープを引く力は50Nです。したがって、仕事率は50×0.5=25(W)です。
理科では単位がとても大切
理科では単位がとても大切です。一方で、そのことを理解できている生徒はほとんどいません。今回の問題みたいな単位の絡む問題で、単位の大切さに気付いてもらいたいものです。
トップ画像=Pixabay




コメント