中学受験理科の計算問題の中でも、ダントツに嫌われるのが「てこのつり合い」です。本記事では、てこの基本的な考え方を解説した後、実際に問題を解いていきます。
2つのつり合いを考える
てこのつり合いの問題では、次の2つのつり合いを考えることが大切です。
- 力のつり合い
- モーメントのつり合い
てこが「つり合う」もしくは「動かない」という状態では、これらの1と2の両方が成立している必要があります。それぞれについて説明します。
力のつり合い
物体にはたらく力の大きさの和が、上と下、左と右などで等しいとき、その物体は動きません。ここでいう「力」には、物体の重さも含まれます。
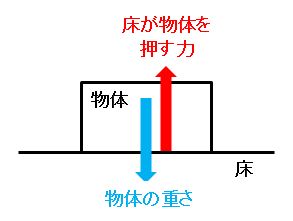
たとえば、下図では、「物体の重さ=床が物体を押す力」が成り立っていれば、物体は動きません。もし、「物体の重さ>床が物体を押す力」ならば、物体は床にめり込みます。逆に、「物体の重さ<床が物体を押す力」ならば、物体は飛び上がります。
モーメントのつり合い
物体は、支点を中心として回転することがあります。しかし、モーメントについて、反時計回りの和と時計回りの和が等しければ、物体は動きません。モーメントとは、次の式で表される大きさです。
小中学校の理科で扱う「てこの原理」の計算は、力のモーメントのつり合いの一種です。
たとえば、下図で赤い▲を支点とするとき、青い矢印で示された左のおもり2つが反時計回りのモーメントで、赤い矢印で示された右のおもり1つが時計回りのモーメントです。
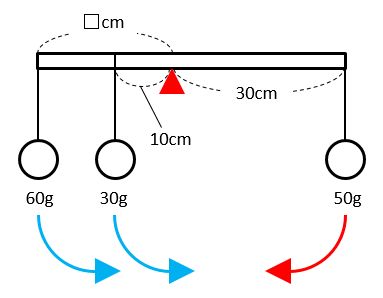
次の式が成り立って、□を求められます。
60×□+30×10=50×30
60×□=1500-300
□=1200÷60=20(cm)
これら2つのつり合いを利用して、実際に問題を解いてみましょう。
てこの基本問題に挑戦
【問題1】下図のように、重さの違うおもりAとBを棒につるしました。そして、この棒をばねはかりにつるしたところ、ばねはかりが300gを示してつり合いました。おもりAの重さが180gで、棒の重さは考えないものとすると、図の□は何cmになりますか。
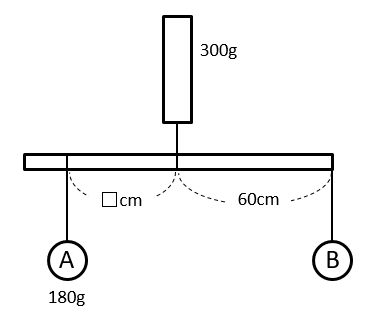
未知のおもりの重さを求める解き方
【問題1】では、おもりBの重さが分かりません。こういう場合は、力のつり合いから、未知のおもりの重さを求めてしまいます。
下向きの力であるおもりAとBと上向きの力であるばねはかりに着目して、力のつり合いの式を作ります。ここでは、Bの重さを△gにしました。
180+△=300
△=300-180=120(g)
続いて、モーメントのつり合いの式を作ります。ここでポイントとなるのは、好きな点を支点にしてOKということです。今回は、ばねはかりの点を支点(赤い▲)にしました。
ちなみに、支点に働く力(重さ)は無視して構いません。というのも、支点との距離が0なので、支点のモーメントは必ず0になるからです。
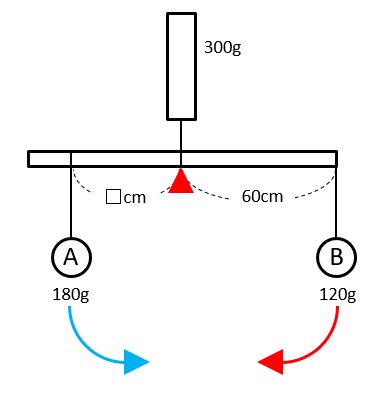
青い矢印(反時計回り)と赤い矢印(時計回り)のモーメントが等しいので、次の式が成り立ちます。
180×□=120×60
□=7200÷180=40(cm)
未知のおもりの重さを求めない解法
【問題1】では、おもりBの重さを求める必要がありません。こういう場合は、おもりBの点を支点(赤い▲)にしましょう。未知のおもりの重さを求める必要がない場合、重さの分からないおもりの点を支点にすると、その重さを無視できるので簡単です。
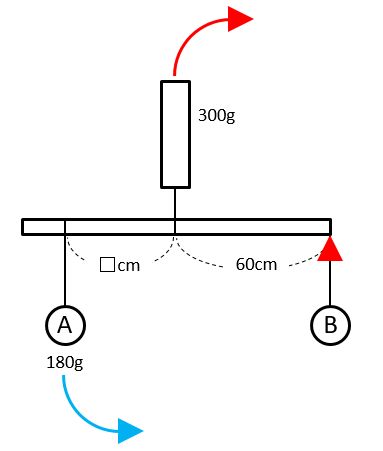
上図のように、青い矢印(反時計回り)と赤い矢印(時計回り)のモーメントが等しいので、次の式が成り立ちます。
180×(□+60)=300×60
180×□+10800=18000
180×□=18000-10800
□=7200÷180=40(cm)
当然ですが、未知のおもりの重さを求めた解法と答は同じです。ただし、支点の位置を変えると、力の向き(反時計回り・時計回り)や力のかかる点と支点との距離が変わります。このことに注意して式を作りましょう。
てこの応用問題に挑戦
【問題2】おもりとひもと棒を使って、下の図のような装置を作りました。この装置がつりあっているとき、次の問いに答えなさい。ただし、ひもと棒の重さは考えなくてよいものとします。
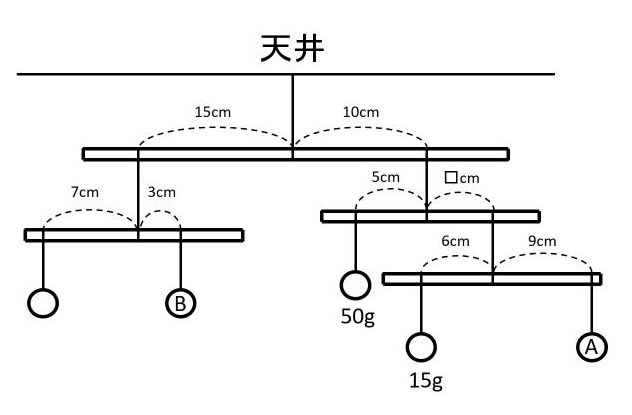
(1) おもりAの重さは何gですか。
(2) 図中の□の長さは何cmですか。
(3) おもりBの重さは何gですか。
【問題2】のように、てこ(滑車や輪軸、ばねなど)が複数組み合わさっている場合、わかる数値をどんどん求めていくことがポイントです。その際、図全体を眺めるのではなく、図の一部に着目して考える必要があります。
(1)の解き方(おもりAの重さを求める)
下図の緑の点線で囲った部分に着目します。
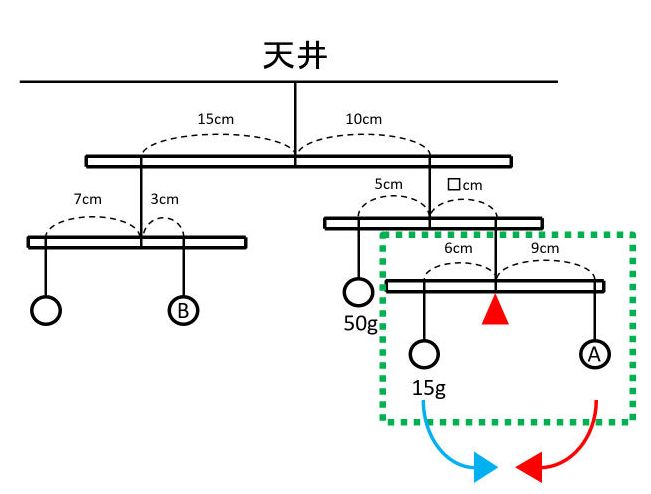
重さ(力)を求める必要のないひもの部分を支点(赤い▲)にして、反時計回り(青い矢印)と時計回り(赤い矢印)を描き込みます。モーメントのつりあいから式を作っておもりAの重さを求めます。
A×9=15×6
A=90÷9=10(g)
(2)の解き方(長さを求める)
下図の緑の点線で囲った部分に着目します。ポイントは、おもりA (10g)と15gのおもりのぶらさがった棒を1つのおもりと考えて25gにしてしまうことです。このように、複数のおもりなどをひとまとめにするという視点はとても役立ちます。
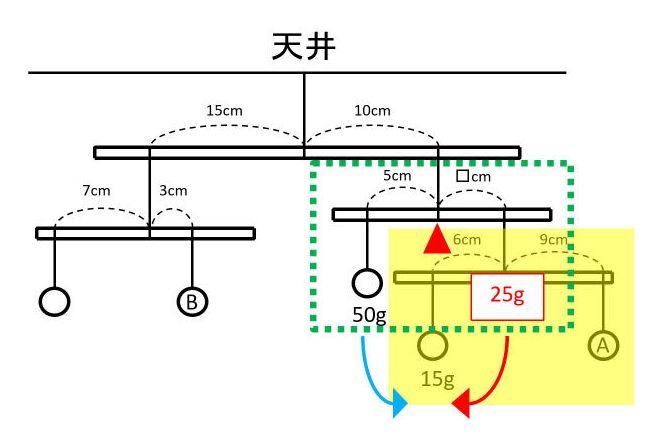
(1)と同様にして、モーメントのつりあいから式を作って□の長さを求めます。
25×□=50×5
□=250÷25=10(cm)
(3)の解き方(おもりBの重さを求める)
(2)までを解いただけではBの重さを求められません。というのも、Bとつりあっている左端のおもりの重さもわからないからです。
このような場合、(1)と(2)で着目した以外の棒に着目します。具体的には、一番上の棒に着目します。図として与えられている情報を全て使うという発想が大切です。
下図の緑の点線で囲った部分に着目します。右側のおもりを1つのおもりと考えて75gにし、左側のおもりを1つのおもりと考えてXにしました。
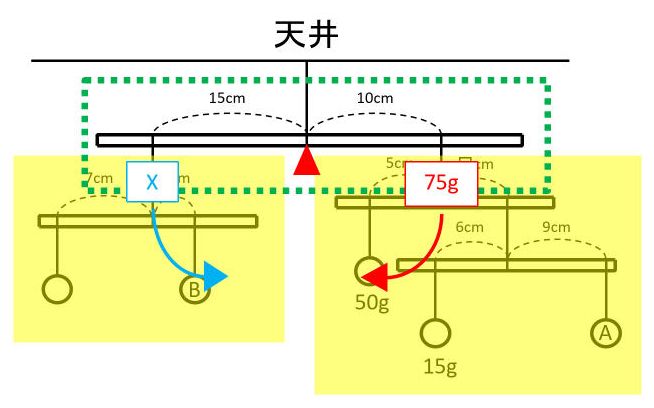
(1)と同様にして、モーメントのつりあいから式を作ってXの重さを求めます。
X×15=75×10
X=750÷15=50(g)
この50gというのは、おもりBと左端のおもりの重さの合計です。このことをふまえて、改めて下図の緑の点線で囲った部分に着目します。左端のおもりをYとしました。
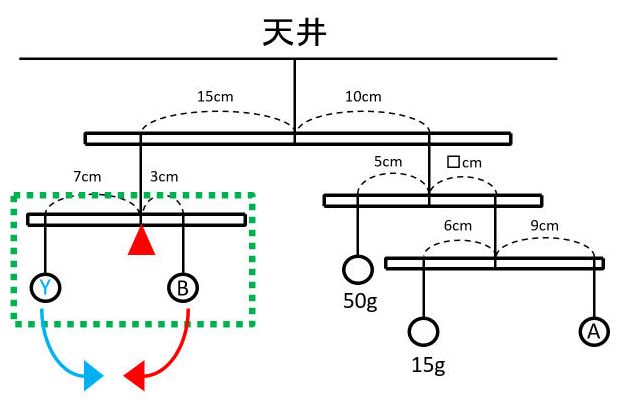
(1)と同様にして、モーメントのつりあいから式を作ります。
B×3=Y×7
これを比の形に直して、
B:Y=7:3
B+Y=50なので、
B=(B+Y)÷(7+3)×7=50÷10×7=35(g)
順を追って数値を求めていけば、複雑なてこの応用問題でも確実に解けます。

てこのつり合いに逆比は要らない
てこのつり合いの計算問題で逆比を使う解法もあります。しかし、複雑な問題で逆比を使おうとすると却って混乱するため、よほどの逆比マニア以外にはお勧めしません。
逆比に頼らず、力のつり合いとモーメントのつり合いから立式して、逆算で解いていく方が確実です。てこのつり合いは慣れれば簡単です。
トップ画像=Pixabay




コメント