【相似比と底辺比】三角形の面積比の求め方をわかりやすく解説するよ

問題演習コーナー

【問題】下の図は、一辺が4cmの正方形とAE=AF=5cmの二等辺三角形を組み合わせたものです。DF=3cmのとき、三角形AFGの面積を求めなさい。

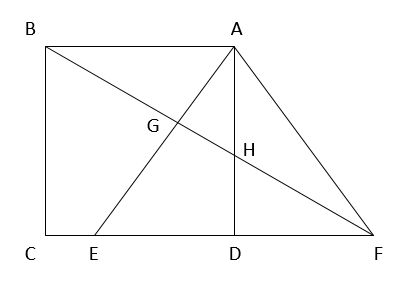
問題文には「三角形AFGの面積を求めなさい」とあるので、素直に「三角形の面積＝底辺×高さ÷2」の公式を思い出しましょう。このとき、長さがわかっている辺を底辺にして、三角形AFGの面積を面積を求められないかを考えます。

AF=5cmですが、高さになりそうな線はありません。補助線を引いて高さにしてもその長さを求められそうにありません。

仕方ないので、三角形AFGを含む図形を探します。このとき、三角形AFGを含む三角形AEFを見つけられれば成功です。

ある図形の面積をすぐに求められないときは、その図形を含む別の図形に目を向けましょう。

とりあえず、わかる情報をどんどん書き込んでいきましょう。

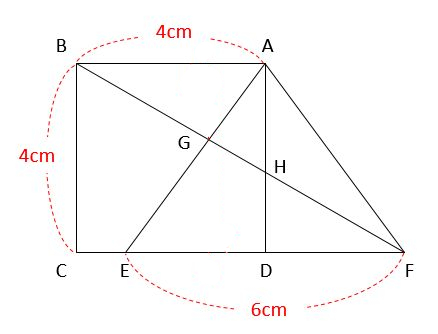
三角形AEFは二等辺三角形なので、DF＝DE＝3cmで底辺EF＝6cmです。高さADは正方形ABCDの一辺なので4cmです。したがって、三角形AEFの面積は6×4÷2＝12（cm²）とわかりました。

正方形ABCDの向かい合う辺は平行なので、ABとCDは平行です。平行線の錯角は等しいので角ABG＝角EFGとなり、三角形ABGと三角形EFGは相似とわかります。相似比は三角形ABG：三角形EFG＝4：6＝2：3なのでAG：EG＝2：3です。

三角形AFGと三角形AEFは高さが共通する三角形なので、底辺比＝面積比です。したがって、AG：EG＝2：3を利用して、三角形AFGの面積＝三角形AEFの面積×\(\frac{2}{2＋3}\)＝12×\(\frac{2}{5}\)＝4.8（cm²）です。

三角形AEFではなく、三角形ABFから面積を求めてもいいでしょう。

三角形ABFの面積は4×4÷2＝8（cm²）です。相似比のBG：FG＝2：3を利用して、三角形AFGの面積＝三角形ABFの面積×\(\frac{3}{2＋3}\)＝8×\(\frac{3}{5}\)＝4.8（cm²）です。

トップ画像＝写真AC