中学受験算数の空間図形では、立方体の切断面を作図する問題がよく出ます。
一見すると難しそうな作図ですが、きちんと手順通りに考えれば簡単です。切り口の多角形を正しく描きましょう。
立方体の切断を2つのルールで考える
立方体の切断は次の2つのルールで考えます。
- 同じ面にある点を結ぶ。
- 向かい合う面の切り口は平行になる。
【例題1】下の立方体を赤い3点を通る平面で切断すると、その切り口はどのような図形になりますか。
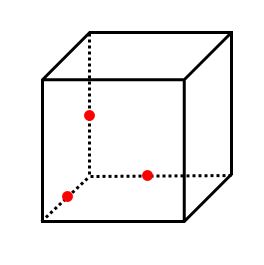
ルール1を使ってそれぞれの点を結ぶと下の図のようになります。
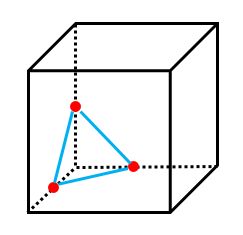
今回はこれで終了です。切り口は三角形になりました。
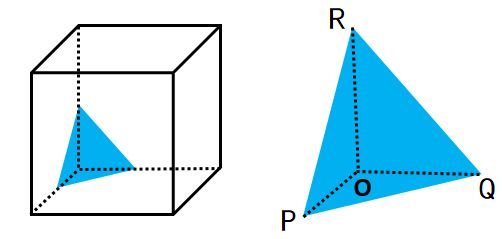
上の図の右は、切り口を1つの面PQRとする三角錐O-PQRを抜き書きしたものです。立方体の切断で複雑そうな場合でも、【例題1】のように三角錐を作ることを考えれば難しくありません。
立方体を切断してできる立体の体積を求める問題については、以下の記事で解説しています。「断頭四角柱」などの体積を求めてみましょう。

切り口が六角形になる場合の作図
【例題2】下の立方体を赤い3点を通る平面で切断すると、その切り口はどのような図形になりますか。
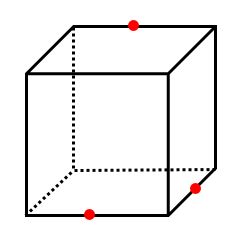
【例題2】では、単純に3点を結んで三角形にしてはいけません。
ルール1を使って、同じ面にある点を結びましょう。そうすると、底面の2点しか結べません。
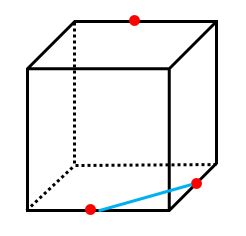
これだけだと切断面がどのような形をしているのかわかりません。
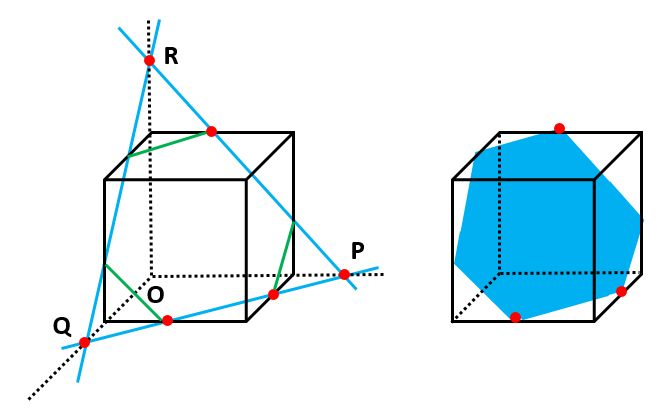
このような場合は、2点を結んだ線分を両側に延長します。さらに、この延長した直線と同じ面で交わるように、立方体の辺(縦と横)も延長します。
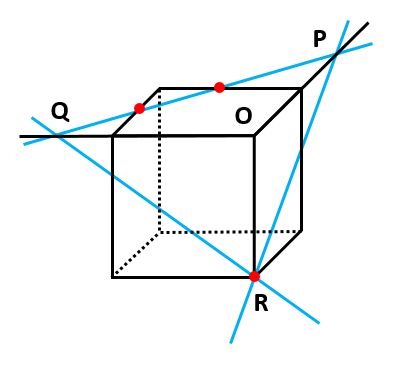
それぞれの直線の交点を下の図のようにP、Qとします。
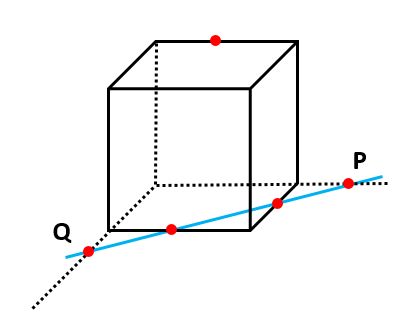
ルール1を使って、Pと同一平面上にある点を結びます。この直線と同じ面で交わるように、立方体の辺(高さ)も延長します。
2本の直線の交点を下の図の通りRとし、その下にある立方体の頂点をOとします。
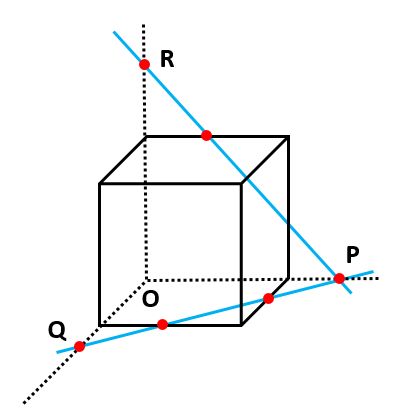
RとQが同じ面にあるので結ぶと、下の図のように三角錐O-PQRが完成します。【例題2】も【例題1】と同じように三角錐を作るのがコツです。
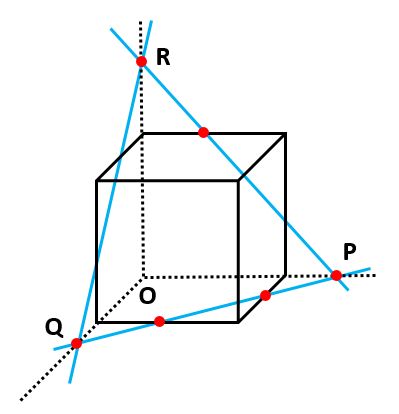
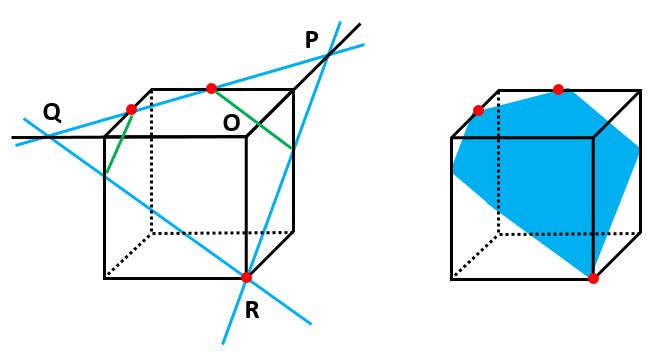
ただ、三角錐O-PQRのままだと、立方体からはみ出しています。そこで、再びルール1を使って同じ面にある点を結ぶ(下の図の左の緑の線)と、切り口が六角形になることがわかりました(下の図の右)。
切り口が五角形になる場合の作図
【例題3】下の立方体を赤い3点を通る平面で切断すると、その切り口はどのような図形になりますか。
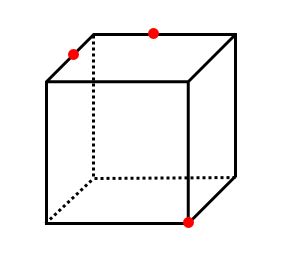
【例題3】の手順も【例題2】と同じなので、解説は省略します。
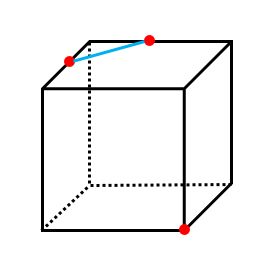
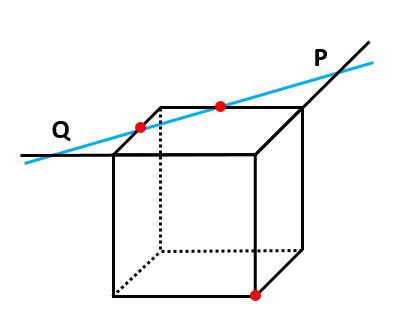
【例題3】でも、三角錐O-PQRを作図しました。そのあと、立方体からはみ出さないようにルール1を使うと、切り口が五角形になることがわかりました。
どの3点も同じ面にない場合の作図
【例題4】下の立方体を赤い3点を通る平面で切断すると、その切り口はどのような図形になりますか。
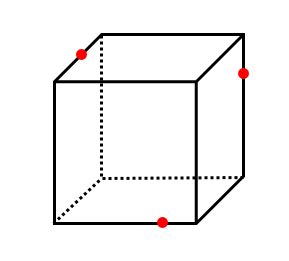
【例題4】では、どの3点も同じ面にないので、ルール1を使えません。
仕方ないので、どの2点でも構わないので、とにかく結んでしまいます。そして、2点を結んだ直線が対角線になるように長方形を作図してPを定めます(下の図)。
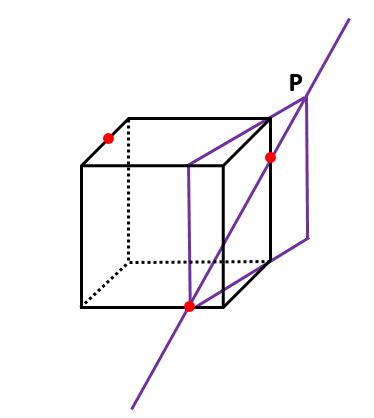
下の図のように、三角錐O-PQRを作図します。【例題1】と同じように三角錐を作る方法が【例題4】でも役に立ちます。
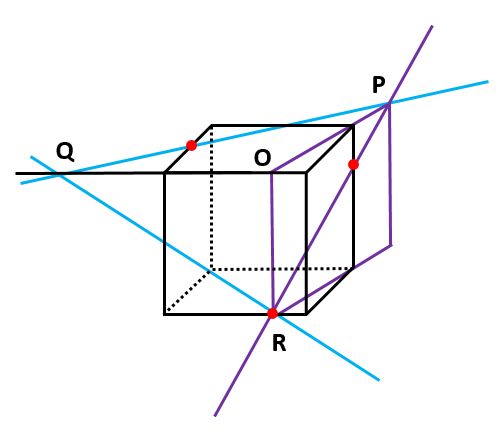
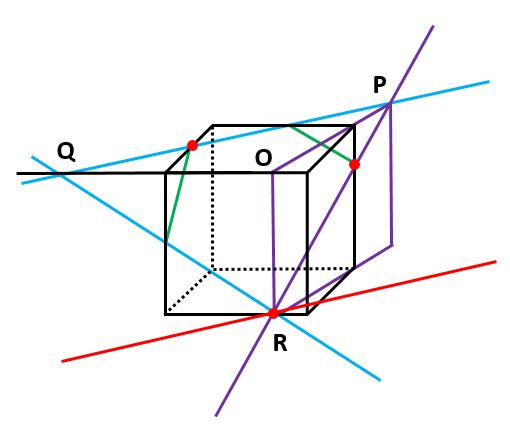
ルール1を使って、立方体の同じ面にある点を結んでいきます(下の図の緑の線)。また、ルール2を使って、直線PQと平行で点Rを通る直線を描きます(下図の赤い直線)。
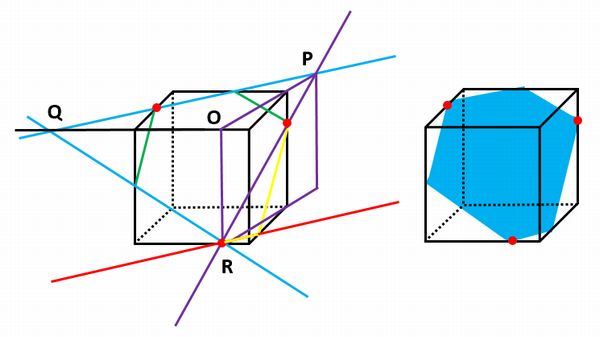
ルール1を使って、赤い直線と立方体の辺との交点と、同じ面にある点と結ぶと(下の図の左の黄色い線)、切り口が六角形になることがわかりました(下の図の右)。
線分と辺を延長して三角錐を作る
立方体の切断面を作図する問題では、ルール1とルール2だけでどうにもならない場合、2点を結んだ線分と立方体の辺を延長して三角錐を作るとよいでしょう。
トップ画像=イラストAC
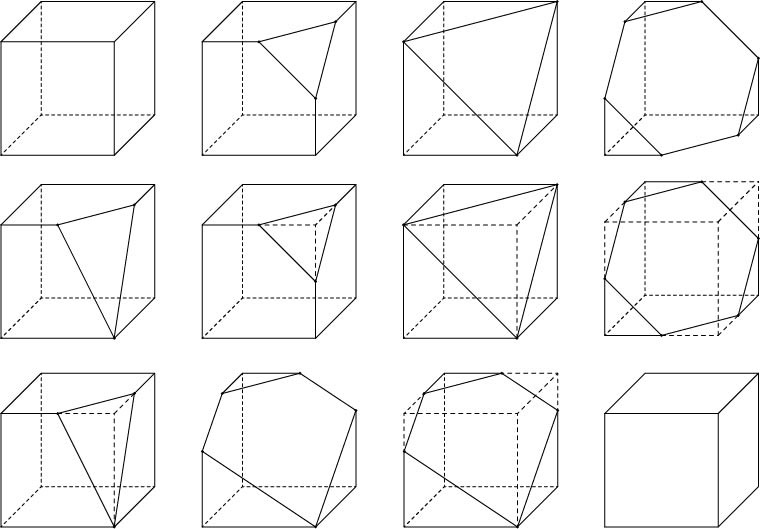



コメント
これすごいわかりやすかった。
おかげさまですぐにやりかたがわかったよ。
コメントありがとうございます。
お役に立ったようでうれしいです。