ある整数を割り切れる整数をその数の「約数」といいます。たとえば、12の約数は、1、2、3、4、6、12です。約数の中には1と自分自身も含まれます。
ある整数の約数を全て求めたい場合、かけてその数になる整数の組み合わせを考えます。6の約数は、1×6、2×3から1、2、3、6の4つです。
実は、ある整数の約数の個数を求めたいだけなら、約数を全て求める必要はありません。素因数分解をすれば約数の個数が分かるからです。
本記事では、素因数分解と約数の個数の関係について解説します。
ある整数を素数の積で表す素因数分解
1より大きい整数の中には、1と自分以外では割り切れない数があります。このような数を「素数」といいます。素数を小さい順から挙げていくと、2、3、5、7、11、13、17、19、23、……です(1は素数から除きます)。
そして、ある整数を素数の積(かけ算)で表すことを「素因数分解」といいます。
たとえば、6を素因数分解すると2×3になります。同じように、他の整数も素因数分解してみましょう。
28=2×2×7
72=2×2×2×3×3
126=2×3×3×7
素因数分解から約数の個数を求めよう
9は1×9、3×3なので、約数は1、3、9の3個です。この「3個」という個数を素因数分解で求めてみましょう。
9を素因数分解すると9=3×3なので、9の約数は1、3、3×3の3個だと分かります。9の約数の個数は(3の個数+1)=3(個)になっています。
同じように、36の約数の個数を求めましょう。
36=2×2×3×3なので、素数の2と3の個数に注目します。2×2の約数は、1、2、2×2の3個です。一方、3×3の約数は、1、3、3×3の3個です。
2×2の約数と3×3の約数の組み合わせを考えると、36の約数は次の9通りです。
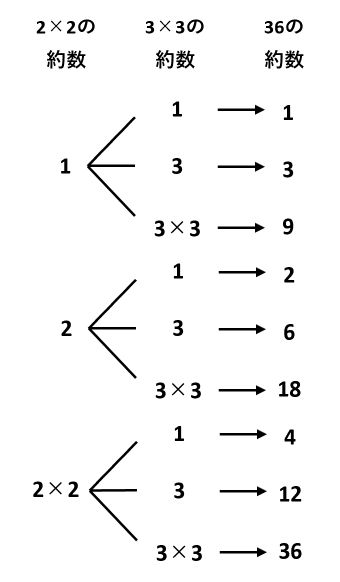
36の約数の個数も(2×2の約数の個数)×(3×3の約数の個数)=(2の個数+1)×(3の個数+1)=3×3=9(個)になっています。
ここまでで分かったことを式にすると次の通りです。
整数Xを素因数分解して、
X=a×a×…×a×b×b×…×b×c×c×…×c(a、b、cは異なる素数)となる場合、
Xの約数の個数=(aの個数+1)×(bの個数+1)×(cの個数+1)

約数の個数を求める問題を解いてみよう
【例題】次の整数の約数の個数をそれぞれ求めなさい。
(1) 16 (2) 63 (3) 500 (4) 2268
それぞれの整数を素因数分解します。
(1)の解答(16の約数の個数を求める)
16=2×2×2×2
2の個数が4個なので、16の約数の個数は4+1=5(個)
(2)の解答(63の約数の個数を求める)
63=3×3×7
3の個数が2個、7の個数が1個なので、63の約数の個数は(2+1)×(1+1)=6(個)
(3)の解答(500の約数の個数を求める)
500=2×2×5×5×5
2の個数が2個、5の個数が3個なので、500の約数の個数は(2+1)×(3+1)=12(個)
(4)の解答(2268の約数の個数を求める)
2268=2×2×3×3×3×3×7
2の個数が2個、3の個数が4個、7の個数が1個なので、2268の約数の個数は(2+1)×(4+1)×(1+1)=30(個)
約数の個数で整数を分類しよう
素因数分解を利用して、約数の個数で整数を分類することもできます。
たとえば、約数の個数が3個の整数は、2×2=4、3×3=9、5×5=25など、同じ素数を2回かけたものです(aを素数とするとa×a)。
一方、約数の個数が4個の整数は、2×2×2=8など、同じ素数を3回かけたものです(aを素数とするとa×a×a)。2×3、3×5など、2種類の素数をかけてできる整数も、約数が4個です(a、bを異なる素数とするとa×b)。
約数の個数で整数を分類すると次の通りです。(表中のa、bは異なる素数)
| 約数の個数 | 整数 | 約数 |
|---|---|---|
| 1個 | 1 | 1 |
| 2個 | a(素数) | 1、a |
| 3個 | a×a | 1、a、a×a |
| 4個 | a×a×a | 1、a、a×a、a×a×a |
| a×b | 1、a、b、a×b | |
| 5個 | a×a×a×a | 1、a、a×a、a×a×a 、a×a×a×a |
| 6個 | a×a×a×a×a | 1、a、a×a、a×a×a 、a×a×a×a、a×a×a×a×a |
| a×a×b | 1、a、b、a×a、a×b、a×a×b |

どんな整数の約数にも1が含まれることを忘れないでね!
1から20までの整数を約数の個数で分類すると次の通りです。
| 約数の個数 | 整数 | 整数の個数 |
|---|---|---|
| 1個 | 1 | 1個 |
| 2個 | 2、3、5、7、11、13、17、19 | 8個 |
| 3個 | 2×2(4)、3×3(9) | 2個 |
| 4個 | 2×2×2(8)、2×3(6)、2×5(10)、2×7(14)、3×5(15) | 5個 |
| 5個 | 2×2×2×2(16) | 1個 |
| 6個 | 2×2×3(12)、2×2×5(20)、2×3×3(18) | 3個 |

素因数分解では、2×3×5や3×3×7×11のように、小さい素数から大きい素数に並べて書くのがコツよ。3×2×5や3×7×3×11のように不規則な書き方をすると、整数の分類で同じ整数を数えたり、数え落としたりするから要注意ね!
約数の個数を求める問題は中学入試でもよく出る
約数の個数に関する問題は中学入試でもよく出ます。全ての約数を求めて個数を数えるのも悪くありませんが、素因数分解から約数の個数を求める方法も覚えておきたいところです。
素因数分解をするならば、どの整数が素数なのかが分かっている必要があります。エラトステネスの篩(ふるい)など、素数を発見する方法も覚えておくといいでしょう。
次の質問に答えましょう。(解答例は最後のページにあります)
① 素因数分解とは何ですか。
② 整数Xを素因数分解して、X=a×a×…×a×b×b×…×b×c×c×…×c(a、b、cは異なる素数)となる場合、Xの約数の個数はどう表せますか。



コメント
ひとつ疑問に思う事があります。それは、約数の個数が4個の場合のときです。同じ素数を3回かけると書いてありますが、22も約数の個数が4個です。しかし、22が同じ素数を3回かけた数であることはおそらくありえない話だと思います。なので、自分なりにまとめてみました。
約数が1個の場合は、1のみ。約数の個数が2個の場合は、素数。約数の個数が3個の場合は、素数の平方数。約数の個数が4個の場合は、違う数の素数をかけた数。
コメントありがとうございます。
洛星志望者さんのまとめで正しいです。
22は、3ページ目に記載したa×bタイプの数です。4ページ目の【問題】(2)も参照していただければと思います。
ご自身で法則性に気づかれたのでしたらとても素晴らしいことです。