【倍数】最小公倍数の求め方は？素因数分解・すだれ算と判定法を解説

問題演習コーナー

【問題1】次の2～3つの数の公倍数を小さい順に3つ求めなさい。

(1)　5、9　　(2)　18、24　　(3)　4、6、9

5と9の両方を割れる数は1しかないので、5と9の最小公倍数は5×9＝45です。

したがって、5と9の公倍数は小さい順に45、90、135です。

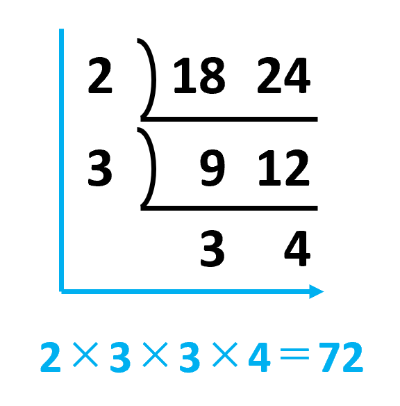
すだれ算から、18と24の最小公倍数は72です。

したがって、18と24の公倍数は小さい順に72、144、216です。

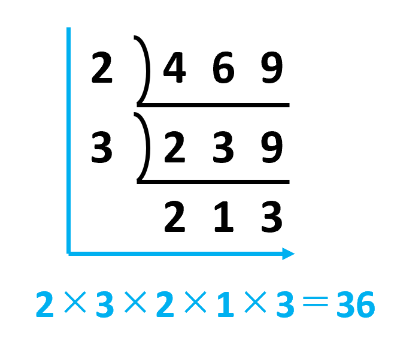
すだれ算から、4と6と9の最小公倍数は36です。

したがって、4と6と9の公倍数は小さい順に36、72、108です。

【問題2】ある駅からA駅行きの電車が4分ごと、B駅行きの電車が8分ごと、C駅行きの電車が10分ごとに発車します。午前7時ちょうどに3台の電車が同時に発車した後、午前10時までに同時に発車する回数は何回ですか。

3台の電車が同時に発車する時刻は、午前7時に4と8と10の最小公倍数を足していくと求められます。

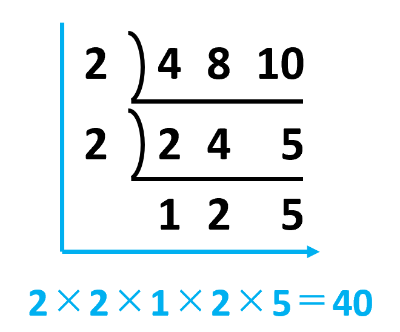
すだれ算から、4と8と10の最小公倍数は40です。

午前7時から午前10時までは3時間あるので、3時間＝180分を40分で割って180÷40＝4あまり20です。午前7時を入れないので4回が答えです。

回数が不安な場合は、午前7時に40分を足していきましょう。午前7時40分→午前8時20分→午前9時→午前9時40分の4回だとわかります。

① 倍数とはどのような数ですか。

（例）ある整数を整数倍した数です。

② 公倍数とはどのような数ですか。

（例）2つ以上の整数に共通する倍数です。

③ 公倍数と最小公倍数の関係を説明しましょう。

（例）公倍数は最小公倍数の倍数です。

トップ画像＝Pixabay