6は2の3倍です。このように、2を整数倍した数を「2の倍数」といいます。
本記事では、倍数の基本、公倍数の求め方、倍数判定法についてわかりやすく解説します。
倍数・公倍数・最小公倍数とは何か?
倍数とは、ある整数を整数倍した数です。たとえば、2の倍数と3の倍数は次の通りです。
- 2の倍数:2、4、6、8、10、12、14、16、18、20、……
- 3の倍数:3、6、9、12、15、18、21、24、27、30、……
2の倍数の中には、2を1倍した2も含まれます。一方で、2を0.5倍した1や、\(\frac{2}{3}\)倍した\(\frac{4}{3}\)など、小数倍した数や分数倍した数は含まれません。
2の倍数と3の倍数では、下線を引いた6、12、18、……が共通します。このように、2つ以上の整数に共通する倍数が公倍数です。
2と3の公倍数の中で最も小さいのが6です。このように、最も小さい公倍数が最小公倍数です。
6、12、18、……を見ると、12は6の2倍、18は6の3倍、……だとわかります。2と3の公倍数に限らず、「公倍数は最小公倍数の倍数」が成り立ちます。
最小公倍数の求め方を理解する
「公倍数は最小公倍数の倍数」なので、公倍数を求めたければ、まずは最小公倍数を求めます。その求め方を紹介します
最小公倍数を素因数分解で求める
2と3の最小公倍数は2×3=6でした。しかし、6と8の最小公倍数は6×8=48ではありません。6の倍数と8の倍数を書き並べると、6と8の最小公倍数は24とわかります。
6の倍数と8の倍数を書き並べずに24を求めてみましょう。
まずは、6と8を素因数分解します。素因数分解とは、ある整数を素数の積(かけ算)で表すことです。

素数は、1と自分以外で割り切れない数だよ。2や3は素数だけど、4は1と4以外に2でも割り切れるから素数じゃないね。

6と8をそれぞれ素因数分解すると、6=2×3、8=2×2×2です。2×3は2×2×2と比べて2×2が不足しています。一方、2×2×2は2×3と比べて×3が不足しています。それぞれに不足分をかけると、どちらも2×2×2×3=24になります。この24が6と8の最小公倍数です。
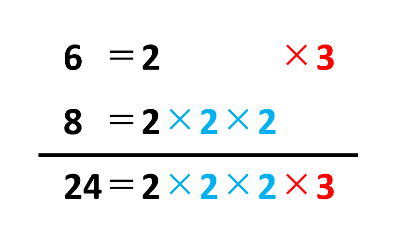
すだれ算(連除法・はしご算)とは何か?
素因数分解を利用した最小公倍数の求め方をもっと簡単にしたのがすだれ算(連除法・はしご算)です。
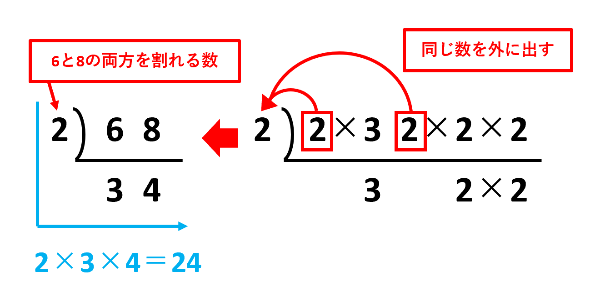
下の図のように、6と8を並べて、割り算の筆算をひっくり返したような計算をします。6と8の両方を割れる2を左に書いて、横棒の下に商の3と4を書きます。3と4の両方を割れる数が1しかないのでここで終了です。最後に、左に書いた2と一番下に書いた3と4をかけて2×3×4=24が6と8の最小公倍数です。
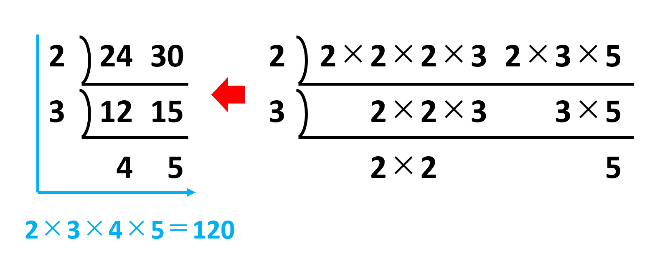
同じように、24と30の最小公倍数は、下のように計算して120です。
3つの整数の最小公倍数をすだれ算で求める
3つの整数の最小公倍数もすだれ算で求められます。
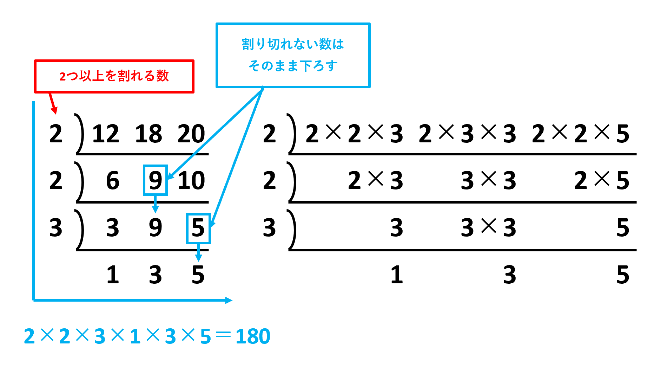
12と18と20の最小公倍数を求めるすだれ算は下の図のようになります。左に書くのは、2つ以上を割れる数です。割り切れなかった数は横棒の下にそのまま下ろします。1と3と5の2つ以上を割れる数が1しかないのでここで終了です。最後に、左に書いた2と2と3と一番下に書いた1と3と5をかけて2×2×3×1×3×5=180が12と18と20の最小公倍数です。
最小公倍数の求め方は最大公約数の求め方とほとんど同じ手順ですが、最後にかける数が違います。また、3つの整数について考える場合、どのような数で割るのかも違います。これらの違いを以下の記事で確認しておきましょう。

2~9の倍数の判定法を知っている?
桁数の多い整数が2~9の倍数かどうかを知りたいときに使える判定法と具体的な整数の例を紹介します。
| 倍数 | 判定法 | 例 |
|---|---|---|
| 2の倍数 | 一の位が偶数(0も偶数) | 320、5638 |
| 3の倍数 | 各位の和が3の倍数 | 123(1+2+3=6)、5217(5+2+1+7=15) |
| 4の倍数 | 下2桁が00か4の倍数 | 700、3724 |
| 5の倍数 | 一の位が0か5 | 820、9635 |
| 6の倍数 | 一の位が偶数で、各位の和が3の倍数 | 432(4+3+2=9)、2154(2+1+5+4=12) |
| 7の倍数 | 一の位を消した数と消した一の位の5倍の和が7の倍数 | 182(18+2×5=28)、2114(211+4×5=231→23+1×5=28) |
| 8の倍数 | 下3桁が000か8の倍数 | 9000、7504 |
| 9の倍数 | 各位の和が9の倍数 | 711(7+1+1=9)、2358(2+3+5+8=18) |

7の倍数の判定法は他にもあるけれど、小学校の算数では習わない負の数が出てくることもあるわ。上で紹介した方法なら暗算でも判定できるんじゃない?

2の倍数は「偶数」といわれることもあるので覚えておきましょう。

倍数の知識を使う問題を整理する
倍数の知識は算数のいろいろな問題を解くときに必要となります。
たとえば、分数の足し算や引き算では通分をしますが、このときに分母を最小公倍数にそろえると計算が楽になります。場合の数で整数を作る問題では、倍数の判定法を知らないと解けないこともあります。
倍数の知識を使う問題を整理しておくことをおすすめします。
次の質問に答えましょう。(解答例は最後のページにあります)
① 倍数とはどのような数ですか。
② 公倍数とはどのような数ですか。
③ 公倍数と最小公倍数の関係を説明しましょう。


コメント