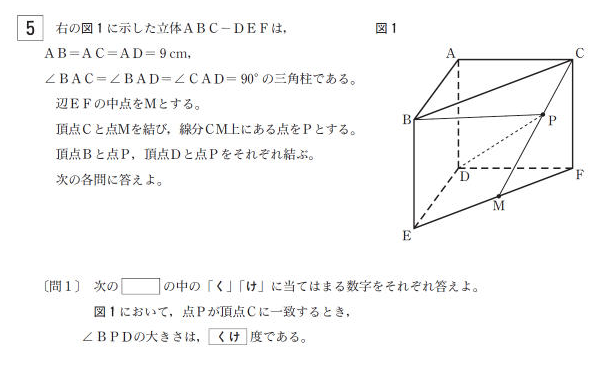
都立高校入試共通問題平成30年度の大問5を解説します。この問題は、例年難しい空間図形問題に比べて、とても簡単な問題でした。
図形が正三角形だと気づければ瞬殺できる問題
[問1]は、例年、図形の性質に気づけば簡単に解ける問題になっています。平成30年度は、その中でも一二を争うくらいの簡単さでした。
PがCに一致しているので、∠BPDは下図の左のようになります。ついでにBとDも結んで△BPDを作ります。△BPDが正三角形になることに気づけるかどうかがポイントです（下図の右）。
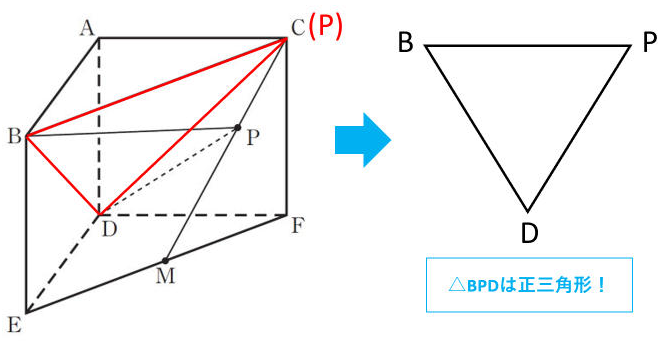
見取り図だと分かりづらいですが、立体ABC-DEFの面ABEDと面ACFDは、一辺が9cmの正方形です。その対角線なのでBD＝CDです。
また、△ABCも、一辺が9cmの正方形を対角線BCに沿って二等分した直角二等辺三角形です。
したがって、BD＝CD＝BCなので、△BPDが正三角形だと分かります。このことに気づけば、一切計算することなく、∠BPD＝60°を求められます。
立体を平面図形に置きかえれば簡単に解ける問題
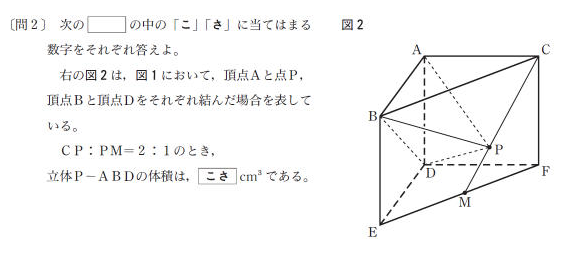
[問2]も、難しい発想は特に必要なく、ちょっとしたことに気づけば簡単です。
立体P-ABDの体積は、素直に△ABDを底面として考えます。高さは、Pから面ABEDに下した垂線PHです。Hの位置は下図のようになります。
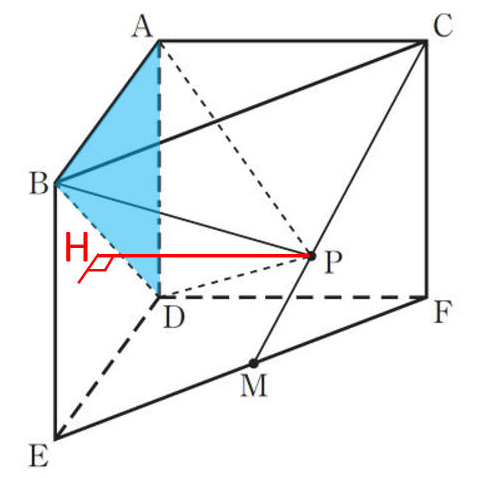
補助線PHを引いたところで、まずは底面を抜き出してみましょう。
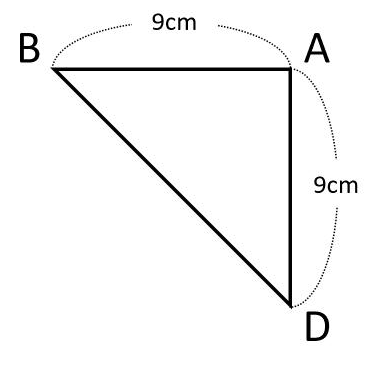
△ABDは、底辺9cm、高さ9cmの直角二等辺三角形なので、面積は9×9÷2＝\(\frac{81}{2}\)（cm2）です。
次に、PH⊥面ABED、∠BAC＝90°から、PHとACが平行であることに気づけるでしょうか？
PHとACが平行だと分かれば、立体を立体のまま考える必要はなくなります。立体ABC-DEFを上から眺めて、下図のように、△ABC上にM、P、Hを全て書き込んでしまいます。
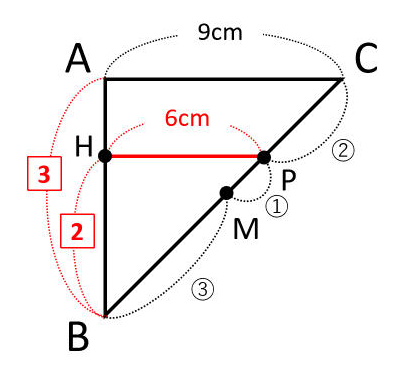
EFとBCは平行で長さが等しいので、Mを真上にあるBCの中点に移動してしまいます。
Pは、CMをCP：PM＝2：1に分けます。このPも真上に移動すると、CP：PM＝2：1となる点と重なります。
BC上の比を考えると、BM＝CM＝CP＋PMなので、BM：MP：PC＝3：1：2です。これより、BC：BＰ＝6：4＝3：2となります。平行線と比の関係から、BA：BH＝BC：BC＝3：2です。
また、平行線の同位角が等しいので∠BAC＝∠BHP、∠BCA＝∠BPHとなり、2組の角がそれぞれ等しいことから、△BAC∽△BHPです。したがって、AC：HC＝BA：BH＝3：2なので、BH＝AC×\(\frac{2}{3}\)＝9×\(\frac{2}{3}\)＝6（cm）です。
立体P-ABDの底面積と高さが分かったので、錐体の体積公式（底面積×高さ÷3）に当てはめて、立体P-ABDの体積は\(\frac{81}{2}\)×6÷3＝81（cm3）です。
前年の大問5の難易度を事前に調べておく
[問2]を言葉で説明すると長くなりますが、発想自体はとても単純で、難しい要素が何もない問題でした。どうしてこんなに簡単な問題になったのでしょうか？
平成29年度の大問5[問2]の正答率があまりにも低かったため、易化の方向に調整したのでしょう。（平成29年度の大問5[問2]の問題と正答率は以下の記事を参照してください）
易化の結果、平成30年度の大問5[問2]の正答率は14.6％に急上昇しました。こうした変化が起こると、次の年は難化に調整されがちです。
大問5[問2]は、年によって難易度の差が激しいという特徴があります。前年が簡単だったか難しかったかについて、過去10年の都立高校入試問題を徹底分析して分野別にまとめた問題集「高校入試 虎の巻
」で事前に調べておき、捨て問にするか頑張って解くかを考えておくとよいでしょう。
トップ画像＝Pixabay
コメント