問題演習コーナー
【問題】ある牧場では、1日に一定の割合で草が生え、牛が1頭ずつ同じ割合で草を食
べています。この牧場に15頭の牛を放すと20日間で草を食べつくし、21頭の牛を放すと12日間で食べつくします。
(1) 草が食べつくされないのは、放した牛が何頭以下のときですか。
(2) 9頭の牛を放すと、何日間で草が食べつくされますか。
(1) 1頭の牛が1日に食べる草の量を1、1日で生える草の量を①とします。
もともと生えていた草の量を左端によせて、「この牧場に15頭の牛を放すと20日間で草を食べつくし、21頭の牛を放すと12日間で食べつくします。」を線分図で表します。
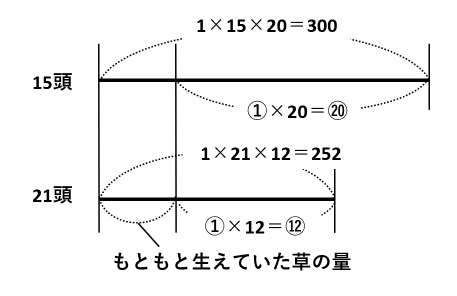
線分図の差(赤い線)に注目します。
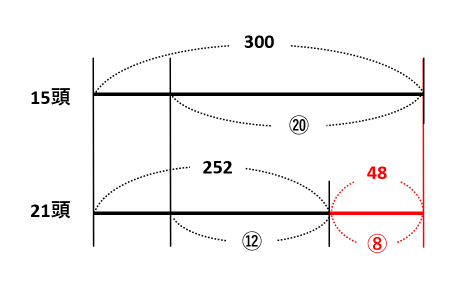 ⑧=48なので、①=48÷8=6です。
⑧=48なので、①=48÷8=6です。
1日で生える草の量は6なので、牛が6頭以下だと1日で生える草の量以下しか食べられず、もともと生えていた草まで食べつくされません。したがって、6頭以下が答です。
(2) もともと生えていた草の量は300-⑳=300-6×20=180とわかりました。
9頭の牛が□日間で草を食べつくすとすると、6×□+180=1×9×□と表せます。9×□-6×□=180より、□=180÷(9-6)=60日間が答です。
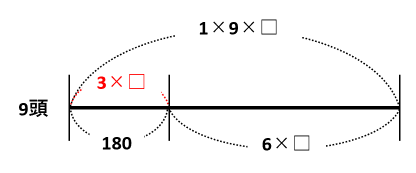
【別解1】消去算
(1) 牛1頭が1日に食べる草の量を1、1日で生える草の量を□、もともと生えていた草の量を△とします。
「生える草の量+もともと生えていた草の量=牛が食べる草の量」なので、□と△で式を作って、消去算で解きます。
「15頭の牛を放すと20日間で草を食べつくし」から、□×20+△=1×15×20 …(ア)です。
「21頭の牛を放すと12日間で食べつくします」から、□×12+△=1×21×12 …(イ)です。
(ア)ー(イ)より□×20-□×12=300-252となり、□=48÷(20-12)=6です。
1日で生える草の量は6なので、牛が6頭以下だと1日で生える草の量以下しか食べられず、もともと生えていた草まで食べつくされません。したがって、6頭以下が答です。
(2) □=6を(ア)に代入して、6×20+△=300となり、△=300-120=180です。
牛1頭が1日に食べる草の量を1とするとき、1日で生える草の量が2、もともと生えていた草の量が180です。
9頭の牛が◇日間で草を食べ尽くすとすると、6×◇+180=1×9×◇となります。9×◇ー6×◇=180より、◇=180÷(9-6)=60なので、60日間が答です。
【別解2】グラフ(ダイヤグラム)
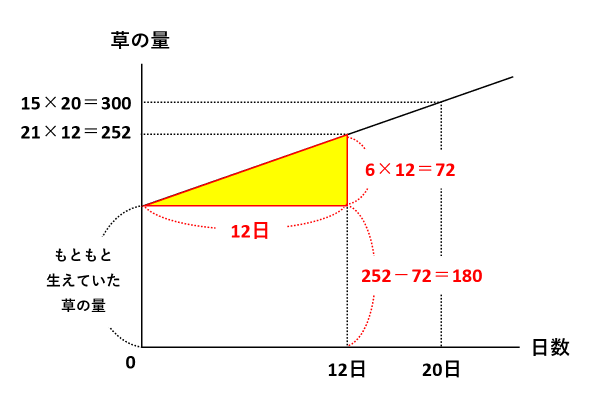
(1) 15頭の牛と21頭の牛がそれぞれ食べつくした草の量と日数を書きこんだのが下の図です。黄色い三角形に注目して、1日で生える草の量は48÷8=6です。
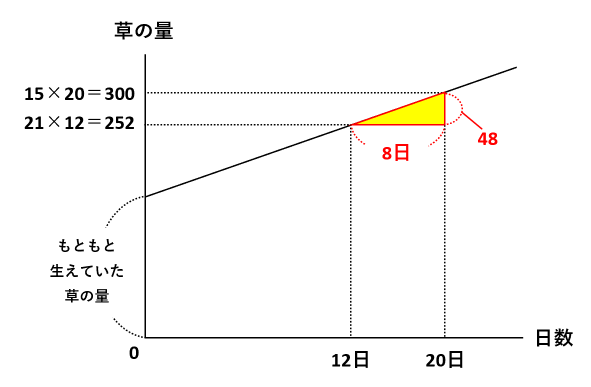
1日で生える草の量は6なので、牛が6頭以下だと1日で生える草の量以下しか食べられず、もともと生えていた草まで食べつくされません。したがって、6頭以下が答です。
(2) 下の図の黄色い三角形に注目して、12日で生える草の量は6×12=72です。したがって、もともと生えていた草の量は252ー72=180とわかります。
9頭の牛が□日間で草を食べつくすとすると、6×□+180=1×9×□と表せます。9×□-6×□=180より、□=180÷(9-6)=60日間が答です。
① 牛が牧草を食べつくす日数を求める問題では、何の量を考えますか。
(例)1日で生える草の量、牛1頭が1日で食べる草の量、もともと生えていた草の量を考えます。
② 牛1頭が1日に食べる草の量をどうしますか。
(例)1にします。
トップ画像=Pixabay



コメント