問題演習コーナー
【問題】花子さんは、60円切手と80円切手を合わせて30枚買う予定でした。しかし、買う枚数をまちがえて逆にしてしまったので、予定より120円高くなりました。60円切手を何枚買う予定でしたか。
予定の代金より実際の代金が高いので、60円切手を多く買う予定だったとわかります。
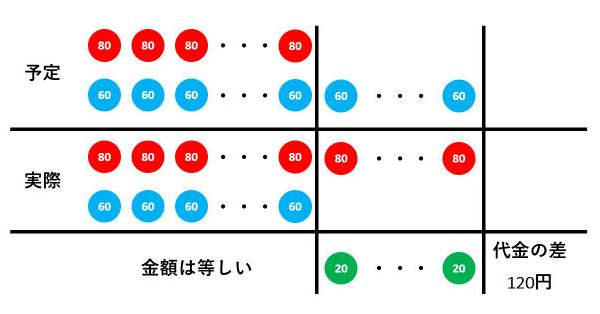
上の表より、60円切手と80円切手の差である20円を集めると、代金の差である120円になります。したがって、実際に多く買ってしまった80円切手の枚数(=多く買う予定だった60円切手の枚数)は、120÷20=6(枚)です。
枚数の合計30枚から多く買った枚数の6枚を引くと24枚です。24枚を半分にすると、実際に買った60円切手の枚数が12枚だとわかります。
したがって、買う予定だった60円切手の枚数は12+6=18(枚)です。
別解1
下の面積図の青い長方形の面積が、代金の差の120円になります。
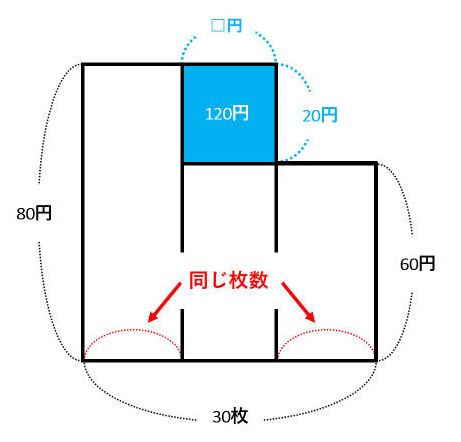
実際に多く買ってしまった80円切手の枚数(=多く買う予定だった60円切手の枚数)は、□=120÷20=6(枚)です。
実際に買った60円切手の枚数は(30-6)÷2=12(枚)なので、買う予定だった60円切手の枚数は12+6=18(枚)です。
別解2
買う予定だった60円切手を□枚、80円切手を△枚とする。
枚数 □+△=30 … ①
代金 60×□+80×△+120=60×△+80×□ … ②
②の式を変形して、
(80-60)×△+120=(80-60)×□
20×△+120=20×□
全体を20で割って、△+6=□ … ③
③を①に代入して、
(△+6)+△=30
2×△=30-6=24
△=24÷2=12なので、□=12+6=18(個)

②の式で、120円は左の式に足すんだよ。まちがえないでね!
・とりちがえ問題では、予定の代金と実際の代金を比べると、どのようなことがわかりますか。
(例)予定の代金より実際の代金が安い場合、単価の高い方を多く買う予定だったとわかります。一方、予定の代金より実際の代金が高い場合、単価の安い方を多く買う予定だったとわかります。
トップ画像=Pixabay



コメント