三角形や四角形などの平面図形を1本の直線のまわりに1回転させたときにできる立体が「回転体」です。
そもそも「図形が回転するのはなぜ?」と思う中学受験生もいるでしょう。しかし、回転して問題になる以上、文句を言っていられません。
今回は、回転体の描き方を紹介した上で、体積や表面積を求めていきます。
回転体の見取り図を描いてみよう
回転の中心となる直線を「回転の軸」といいます。
たとえば、下の△ABCを、ABを回転の軸として1回転させると円錐になります。
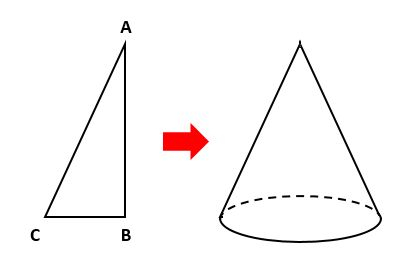
回転後の図形を立体的に描いた右の図が「見取り図」です。
回転体の見取り図を簡単に描くためのコツを紹介します。
例として、下の四角形を、直線ℓを回転の軸として1回転させてできる立体の見取り図を描いてみましょう。
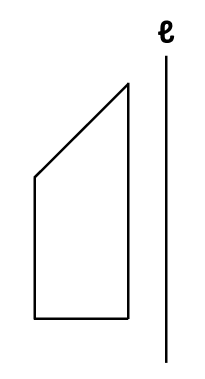
どのような立体になるか、イメージできますか?
イメージできなくても、これから紹介する手順に従えば、回転体の見取り図を誰でも簡単に描けます。
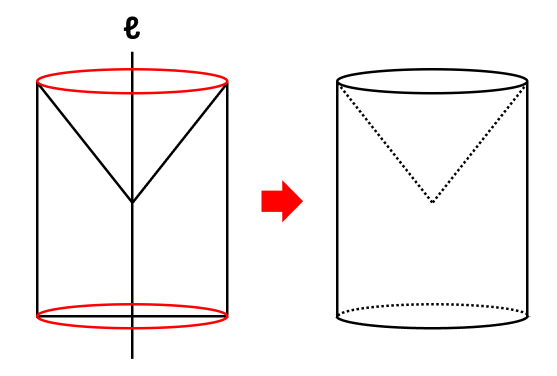
図形を回転の軸に対して対称移動させる
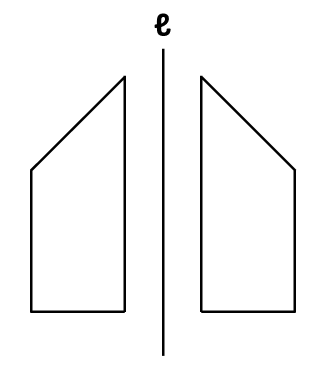
直線ℓの左にある四角形を、回転の軸ℓに対して右に対称移動させます。
対称移動とは、「対称の軸」と呼ばれる直線を中心として、左右が逆になるように図形を移動させることです。対称の軸を折り目として折ると、左右の図形がぴったり重なります。
例では、回転の軸ℓが対称の軸です。
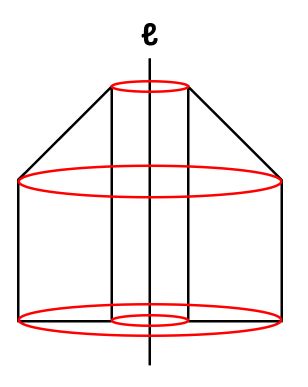
左右の図形の頂点を楕円で結ぶ
左右の図形の対応する頂点同士を楕円(下の図の赤い線)で結びます。
対応する頂点とは、対称の軸を折り目として折ったときにぴったり重なる頂点のことです。
どんな立体になるかがわかるなら、これで終了です。さらに分かりやすい見取り図にしたければ、次の手順に進みましょう。
不要な線を消して見取り図を完成させる
底面の半径や直線ℓなどの不要な線を消します。
また、外から見える線を実線にして、外から見えない線を点線にします。
今回の例では、下の見取り図を描けるはずです。鉛筆から芯を抜いたような立体図形になりました。
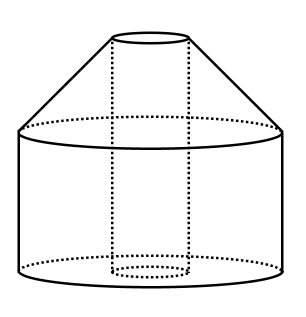
回転体の体積や表面積を求めよう
回転体の見取り図を描けるようになったところで、体積や表面積を求めていきましょう。
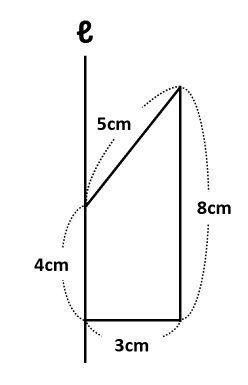
回転体の見取り図を描くと下のようになります。
右の見取り図から、回転体は円柱から円錐を引いた立体であることがわかりました。
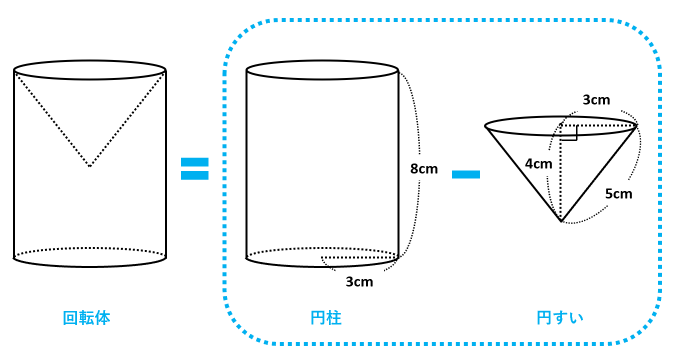
回転体の体積を求めよう
体積を求めるのは簡単です。
回転体の表面積を求めよう
表面積を求めるのが少し大変です。
円柱と円すいの展開図を描いて、どの部分の面積が回転体の表面積に含まれるのかを確認しましょう。
まず、円柱については、上の底面積を除き、下の底面積と側面積が表面積に含まれます。
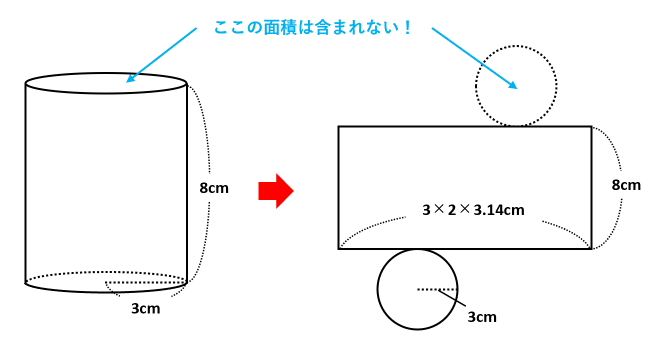
次に、円すいについては、底面積を除き、側面積だけが表面積に含まれます。
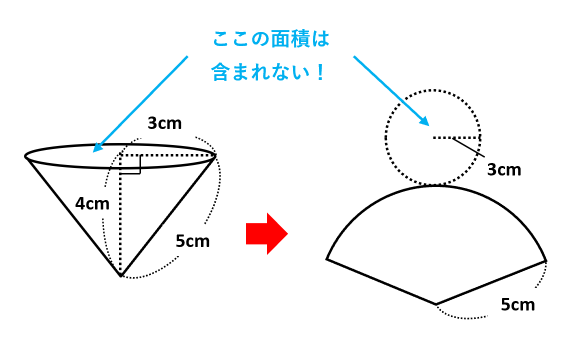

円すいの側面積は「母線×母線×3.14×\(\frac{底面の円の半径}{母線}\)」で求められるよ。上の円すいでは、5cmの線が母線だね。

おうぎ形の面積は「弧の長さ×母線×\(\frac{1}{2}\)」でも求められるから、3×2×3.14×5×\(\frac{1}{2}\)でも同じ結果になるわ。弧の長さは底面の円の円周の長さに等しいのよ。
回転体は図を描くことでわかりやすくなる
回転体の問題では、見取り図や展開図を描いたり、変な形の立体を柱体やすい体に分けて描き直したりするとわかりやすくなります。
頭の中で考えると混乱することが多いので、図を描くことを大切にしてください。



コメント