形が同じで大きさが違う図形同士の関係を「相似」といいます。特に「2組の角がそれぞれ等しい」(相似条件)が成り立つ2つの三角形は相似です。
本記事では、相似な三角形の辺の長さを求める問題のコツを解説します。
ちょうちょかピラミッドを見つけよう
相似な三角形の辺の長さを求める問題では、ちょうちょかピラミッドを見つけることが大切です。
ちょうちょとはどのような図形か?
ちょうちょは下の図形です。「クロス」「砂時計」などと呼ばれることもあります。
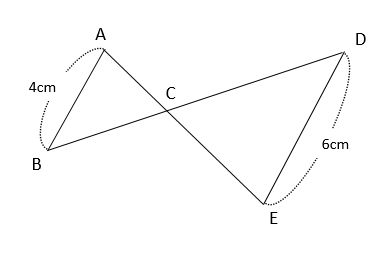
この図形では、ちょうちょの羽の両端であるABとDEが平行ならば、三角形ABCと三角形EDCは相似です。なぜなら、平行線の錯角が等しいので角BAC=角DEC、角ABC=角EDCとなり、「2組の角がそれぞれ等しい」が成り立つからです。

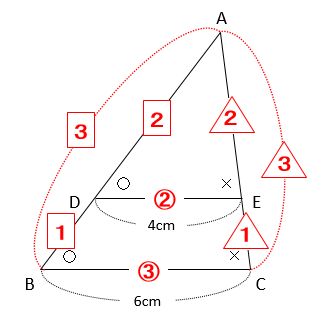
三角形ABCと三角形EDCの対応する角(同じ大きさの角)に印を付けたのが下の図です。
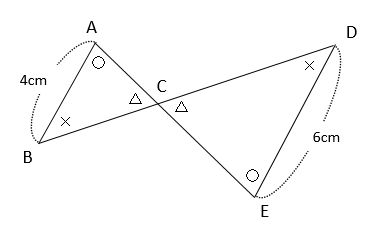
この図では、○と×に挟まれているABとEDが対応する辺なので、相似比はAB:ED=4:6=2:3です。したがって、AB:ED=BC:DC=CA:CE=2:3です。
図に相似比を書き込みましょう。相似比は同じでも辺の長さが違うので、それぞれの比を○□△で囲いました。
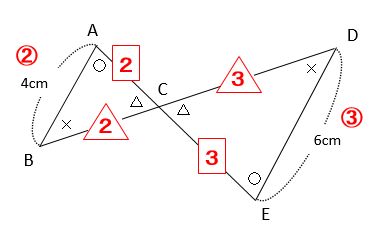
ちょうちょでは、AC:EC=2:3のように、相似比が交差することに注意しましょう。AC:DC=2:3ではありません。
ピラミッドとはどのような図形か?
ピラミッドは下の図形です。
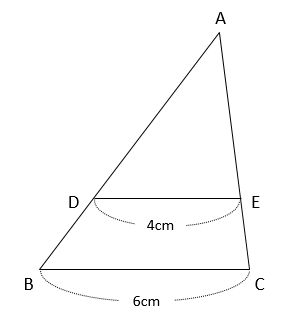
この図形では、ピラミッドの土台であるBCとDEが平行ならば、三角形ABCと三角形ADEは相似です。なぜなら、平行線の同位角が等しいので角ABC=角ADE、角ACB=角AEDとなり、「2組の角がそれぞれ等しい」が成り立つからです。

ちょうちょと同じように、三角形ABCと三角形ADEの対応する角に印を付け、相似比を書き込んだのが下の図です。
相似比はBC:DE=6:4=3:2なので、BC:DE=AB:AD=AC:AE=3:2です。また、AD:DB=AE:EC=2:1も成り立ちます。
ピラミッドでは、AD:DB=2:1につられてDE:BC=2:1にしてはいけません。
ちょうちょとピラミッドの組み合わせ問題
多くの中学受験生が悩む有名問題を解いてみましょう。
【例題】下の図で、ABとDEとCFは平行です。AB=10cm、DE=15cmのとき、CFの長さを求めなさい。
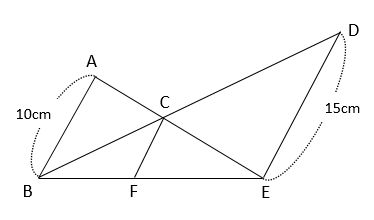
【例題】はちょうちょとピラミッドの両方を使って解きます。
まずは、ちょうちょとピラミッドを見つけて抜き書きしましょう。複雑な図形は、自分が理解しやすいように描き直すことが大切です。
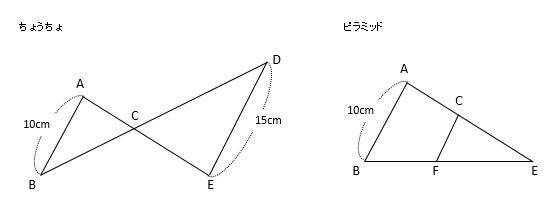
次に、これらの図に対応する角の印と相似比を書き込みます。
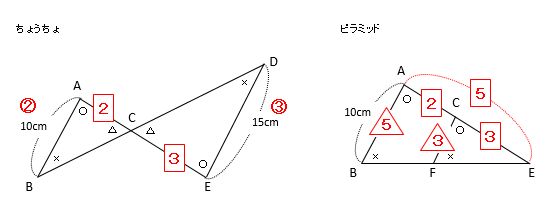
ちょうちょの羽の両端の長さが分かっているので、三角形ABCと三角形EDCの相似比はAB:ED=10:15=2:3です。したがって、ピラミッドの辺の比もAC:CE=2:3とわかりました。
ピラミッドを見て、AC:CE=2:3から、三角形ABEと三角形CFEの相似比はAE:CE=AB:CF=5:3です。したがって、10:CF=5:3より、CF=10×3÷5=6(cm)が答えです。
相似な三角形の問題を考えるための3ステップ
相似な三角形の問題では、多くの場合、ちょうちょかピラミッドを利用します。このタイプの問題は次の3ステップで考えましょう。
- ちょうちょかピラミッドを探す。
- 1で見つけたちょうちょやピラミッドを抜き書きする。
- 2の図に、対応する角の印と相似比を書き込む。
相似比だけでなく底辺比も使う問題になると難しくなりますが、それでも相似が関係するなら上の3ステップは有効です。
トップ画像=Pixabay

コメント