多くの小学生は割り算でつまずきます。小学生にとって、割り算の何が難しいのでしょうか?
彼らの計算過程を分析してみましょう。
小学生にとって割り算が難しい理由
割り算の難しさとして考えられるのは次の2点です。
- 筆算の形式が今までと異なる。
- 足し算・引き算・かけ算の全てを使う。
とはいえ、この2点は慣れの問題です。くり返し練習すれば、ほとんどの小学生はできるようになります。
一方、次の点は見落とされがちですが、多くの生徒たちのつまずきポイントとなっています。
生徒たちは割り算の筆算方法を知っています。それにもかかわらず、商をいつまでも決定できず、グチャグチャ頭の中で考えているうちに「割り算わかんない」となってしまいます。
割り算をかけ算の逆演算と考えると…
たとえば567÷24を考えましょう。
割り算を苦手とする生徒は「24に何をかけると567になるんだろう?」と考えます。紙の隅で24×25や24×31などの筆算を頑張る生徒もいます。
確かに、割り算はかけ算の逆演算です。24×□=567を満たす□をしらみつぶしに探していく方法も決して間違いではありません。しかし、この方法は時間がかかり過ぎる上に面倒です。もっと効率的な方法を使わないと、「割り算が苦手」を克服できません。
では、どうすれば効率的に商を決定できるのでしょうか?
割る数と割られる数を比べる方法
「割り算が苦手」と悩む生徒には「割る数と割られる数の左側の数字を比べなさい」と教えるとよいでしょう。具体的には、次の2つの数字を見比べさせます。
- 割る数の最上位の数字 → ①
- 割られる数の上位1~2桁 → ②
「①を何倍すると②になるか?」を考えさせます。
【例1】567÷24の筆算
567÷24の筆算を例に考えましょう。
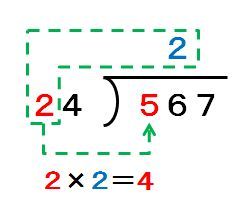
まずは、56÷24を計算して、割られる数の6の上に数字を書きます。このとき、次のように①と②に具体的な数値を当てはめます。
- 割る数の最上位の数字 → 2
- 割られる数の上位1桁 → 5
2×2≒5なので、6の上には2を書きます。このとき、2×3としないでください。計算した結果が、5より大きくなってしまうからです。
次に、87÷24です。割る数と割られる数の最上位の数字を見比べて、割られる数の”7″の上に4を書きます。
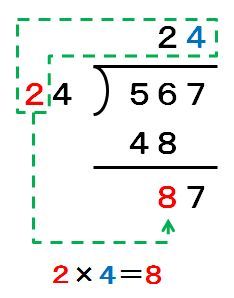
しかし、24×4=96は87より大きいので引けません。こういう場合は、4から1を引いて3に書き換えます。
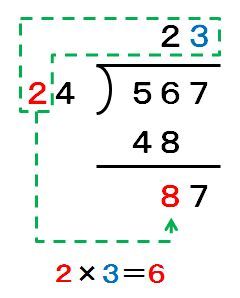
24×3=72は87より小さいので、87-72=15となって、商の23と余りの15を求められました。
【例2】547÷69の筆算
547÷69の筆算も考えてみましょう。
割る数と割られる数の最上位の数字を比べると、割る数の方が6で、割られる数の方が5です。6の方が5より大きいので、割られる数の上位2桁の54を考えることにします。
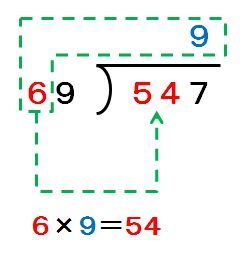 9と見当を付けてみますが、計算してみると69×9=621となって547から引けません。621から69を1回引いても547より大きな数となるので、9の代わりに書くべき数字は、8ではなく7です。
9と見当を付けてみますが、計算してみると69×9=621となって547から引けません。621から69を1回引いても547より大きな数となるので、9の代わりに書くべき数字は、8ではなく7です。
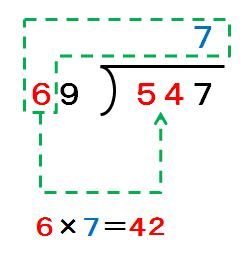
69×7=483なので、547-483=64となり、商の7と余りの64を求められました。
ちなみに、69は70に近い数です。こういうときは、69を70にしてしまって547÷70と考えると、商を楽に求められます。概数(およその数)を使った計算方法も知っておくと便利です。
「割り算が苦手」から「割り算が得意」へ
ここまでで紹介した計算方法を教わった生徒たちは、ほとんどが「割り算が苦手」から「割り算が得意」に大変身します。ちょっとしたコツで苦手意識がなくなると、目がキラキラ輝かせながら割り算の筆算をするようになります。
トップ画像=フリー写真素材ぱくたそ / モデル=ゆうき



コメント
とてもわかりやすかったです!!!